Cho điểm \(A\left( {2;1} \right)\). Tìm điểm $B$ trên trục hoành và điểm $C$ trên đường phân giác của góc phần tư thứ nhất để chu vi tam giác $ABC$ nhỏ nhất.
Trả lời bởi giáo viên
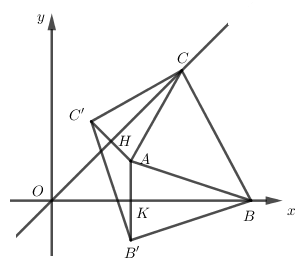
Gọi $B',C'$ lần lượt là điểm đối xứng với $A$ qua trục $Ox$ và đường thẳng $y = x$ ta có : \(AB = BB',AC = CC'\)
Dễ thấy \(B'\left( {2; - 1} \right)\)
$AC'$ là đường thẳng đi qua $A$ và vuông góc với đường thẳng $y = x$ nên có phương trình $x + y-3 = 0$.
Gọi $H$ là giao điểm của đường thẳng $y = x$ và \(x + y-3 = 0 \Rightarrow H\left( {\dfrac{3}{2};\dfrac{3}{2}} \right)\) là trung điểm của \(AC' \Rightarrow C'\left( {1;2} \right)\)
Chu vi tam giác $ABC$ là :
\(\begin{array}{l}C = AB + BC + CA = B'B + BC + CC' \ge B'C'\\ \Rightarrow {C_{\min }} = B'C' \Leftrightarrow B = Ox \cap B'C',\,\,C = \left( {y = x} \right) \cap B'C'\end{array}\)
Phương trình $B'C'$:
\(\dfrac{{x - 2}}{{1 - 2}} = \dfrac{{y + 1}}{{2 + 1}} \Leftrightarrow - x + 2 = \dfrac{{y + 1}}{3} \Leftrightarrow - 3x + 6 = y + 1 \Leftrightarrow 3x + y - 5 = 0\)
\( \Rightarrow B\left( {\dfrac{5}{3};0} \right),C\left( {\dfrac{5}{4};\dfrac{5}{4}} \right)\)
Hướng dẫn giải:
Gọi $B',C'$ lần lượt là điểm đối xứng với $A$ qua trục $Ox$ và đường thẳng $y = x$ ta có : \(AB = BB',AC = CC'\)
\(C = AB + BC + CA = B'B + BC + CC' \ge B'C' \Rightarrow {C_{\min }} = B'C' \Leftrightarrow B = Ox \cap B'C',C = \left( {y = x} \right) \cap B'C'\)

