Câu hỏi:
2 năm trước
Cho \(\Delta ABC\) có \(M\) là trung điểm của \(BC\). Trong các khẳng định sau khẳng định nào đúng?
Trả lời bởi giáo viên
Đáp án đúng: b
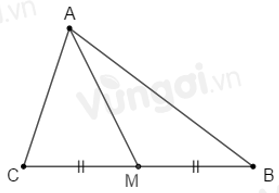
Nối đoạn thẳng AM.
Xét \(\Delta AMC\) có: \(AM < AC + CM\) (bất đẳng thức tam giác) (1)
Xét \(\Delta AMB\) có: \(AM < AB + MB\) (bất đẳng thức tam giác) (2)
Vì \(M\) là trung điểm của \(BC\) (gt) nên \(M\) nằm giữa \(B\) và \(C\) ta có: \(CM + MB = BC.\)
Cộng bất đẳng thức (1) và (2) theo vế với vế ta được:
\(\begin{array}{l}AM + AM < AC + CM + AB + MB\\ \Rightarrow 2AM < AB + \left( {CM + MB} \right) + AC\\ \Rightarrow 2AM < AB + BC + AC\\ \Rightarrow AM < \dfrac{{AB + BC + AC}}{2}\end{array}\)
Do đó \(AM\) nhỏ hơn nửa chu vi của tam giác \(ABC\).
Hướng dẫn giải:
- Nối đoạn thẳng AM.
- Áp dụng bất đẳng thức tam giác chứng minh: \(AM < AC + CM\), \(AM < AB + MB\). Từ đó lập luận suy ra điều phải chứng minh.
Câu hỏi khác
- Đề kiểm tra giữa học kì 1 - đề số 1 Toán 7 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 - đề số 3 Toán 7 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 - đề số 1 Toán 7 có lời giải chi tiết
- Đề kiểm tra giữa học kì 1 - đề số 2 Toán 7 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 - đề số 1 Toán 7 có lời giải chi tiết
