Câu hỏi:
2 năm trước
Cho ^AOB=300. Vẽ tia OC là tia đối của tia OA. Tính ^COD biết OD⊥OB, các tia OD và OA thuộc hai nửa mặt phẳng đối nhau bờ OB.
Trả lời bởi giáo viên
Đáp án đúng: d
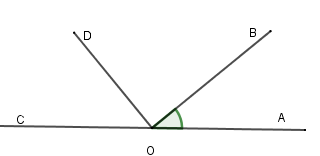
Vì OD⊥OB nên ^DOB=90∘.
Vì OA và OC là hai tia đối nhau và tia OB nằm giữa OA và OD nên ta có
^AOB+^DOB+^COD=^AOC⇒30∘+90∘+^COD=180∘⇒^COD=180∘−120∘⇒^COD=60∘.
Vậy ^COD=60∘.
Hướng dẫn giải:
Sử dụng tính chất cộng góc và góc bẹt có số đo 180∘.