Câu hỏi:
3 năm trước
Cho \(\widehat {AOB} = 100^\circ \). Vẽ tia \(OC\) sao cho tia \(OB\) nằm giữa hai tia \(OA\) và \(OC\) đồng thời \(\widehat {COB} = {30^0}\). Tính số đo \(\widehat {AOC}\).
Trả lời bởi giáo viên
Đáp án đúng: b
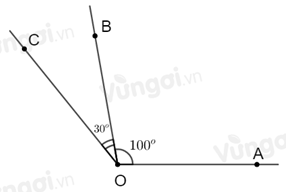
Vì tia \(OB\) nằm giữa hai tia \(OA\) và \(OC\) nên \(\widehat {AOB} + \widehat {BOC} = \widehat {AOC}\) .
Mà \(\widehat {AOB} = {100^o}\); \(\widehat {COB} = {30^0}\) suy ra \(\widehat {AOC} = {100^o} + {30^o} = {130^o}.\)
Hướng dẫn giải:
Sử dụng công thức cộng góc: Nếu tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\) thì \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}.\)