Câu hỏi:
2 năm trước
Cho 4 điểm không đồng phẳng A,B,C,D. Gọi I,K lần lượt là trung điểm của AD và BC. Giao tuyến của (IBC) và (KAD) là:
Trả lời bởi giáo viên
Đáp án đúng: a
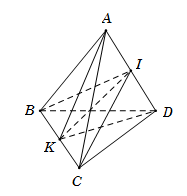
Điểm K là trung điểm của BC suy ra K∈(IBC)⇒IK⊂(IBC).
Điểm I là trung điểm của AD suy ra I∈(KAD)⇒IK⊂(KAD).
Vậy giao tuyến của hai mặt phẳng (IBC) và (KAD) là IK.
Hướng dẫn giải:
- Chứng minh I,K thuộc cả hai mặt phẳng, từ đó suy ra IK là giao tuyến.