Câu hỏi:
2 năm trước
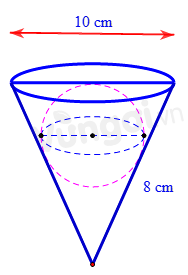
Bạn An có một cốc hình nón có đường kính đáy là 10cm và độ dài đường sinh là 8cm. Bạn dự định đựng một viên bị hình cầu sao cho toàn bộ viên bi nằm trong cốc (không phân nào của viên bị cao hơn miệng cốc). Hỏi bạn An có thể đựng được viên bị có đường kính lớn nhất bằng bao nhiêu?
Trả lời bởi giáo viên
Đáp án đúng: c
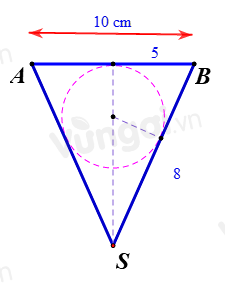
Bước 1: Xét thiết diện qua trục.
Thiết diện qua trục là một tam giác cân có cạnh bên là 8cm và cạnh đáy là 10 cm (tam giác SAB)
Bước 2: Xác định vị trí của viên bi thỏa mãn bài toán
Viên bi bị cắt theo chính thiết diện đó thì sẽ tiếp xúc với hai cạnh bên.
Viên bi càng tiến gần đáy thì càng lớn.
Để viên bị có đường kính lớn nhất thì viên bi phải tiếp xúc với mặt trên của cốc nước (miễn là viên bi không cao hơn miệng cốc)
Bước 3: Tính đường kính viên bi
\(p = \dfrac{{8 + 8 + 10}}{2} = 13\)
\(\begin{array}{l}r = \dfrac{S}{p} = \dfrac{{5\sqrt {{8^2} - {5^2}} }}{{13}} = \dfrac{{5\sqrt {39} }}{{13}}\\d = 2r = \dfrac{{10\sqrt {39} }}{{13}}\left( {cm} \right)\end{array}\)
Hướng dẫn giải:
Bước 1: Xét thiết diện qua trục.
Bước 2: Xác định vị trí của viên bi thỏa mãn bài toán
Bước 3: Tính đường kính viên bi
Áp dụng công thức tính bán kính đường tròn nội tiếp \(r = \dfrac{S}{p}\) với \(p = \dfrac{{a + b + c}}{2}\)
