Câu hỏi:
3 năm trước
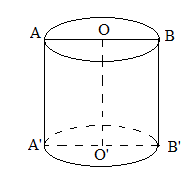
Xét hình trụ \(T\) có thiết diện qua trục của hình trụ là hình vuông cạnh $a$. Tính diện tích toàn phần \(S\) của hình trụ.
Trả lời bởi giáo viên
Đáp án đúng: a
Ta có: \(r = OA = \dfrac{{AB}}{2} = \dfrac{a}{2};h = AA' = a\) nên \({S_{tp}} = 2\pi rh + 2\pi {r^2} = 2\pi .\dfrac{a}{2}.a + 2\pi .{\left( {\dfrac{a}{2}} \right)^2} = \pi {a^2} + \dfrac{{\pi {a^2}}}{2} = \dfrac{{3\pi {a^2}}}{2}\)
Hướng dẫn giải:
Công thức tính diện tích toàn phần hình trụ: \({S_{tp}} = {S_{xq}} + 2.{S_d} = 2\pi rh + 2\pi {r^2}\)