Vật trượt từ đỉnh mặt phẳng nghiêng nhãn dài \(l = 10m\), góc nghiêng \(\alpha  = {30^0}\) . Hỏi vật tiếp tục chuyển động trên mặt phẳng ngang bao lâu khi xuống hết mặt phẳng nghiêng, biết hệ số ma sát với mặt phẳng ngang là \(\mu  = 0,1\).

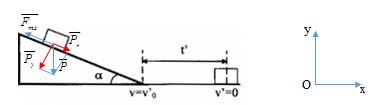
+ Gắn hệ trục tọa độ như hình vẽ

+ Viết phương trình định luật II – Niuton cho vật ta được:

\(\overrightarrow P  + \overrightarrow {{F_{ms}}}  = m\overrightarrow a \) (1)

+ Chiếu (1) lên các phương ta được:

Ox: \({P_x} - {F_{ms}} = ma \to a = \dfrac{{{P_x} - {F_{ms}}}}{m} = \dfrac{{P\sin \alpha  - \mu P\cos \alpha }}{m} = g\sin \alpha  - \mu g\cos \alpha \)

+ Vì mặt phẳng nghiêng nhẵn nên hệ số ma sát bằng \(0\), do đó: \(a = g.\sin \alpha  = 10.\sin {30^0} = 5m/{s^2}\)

+ Vận tốc của vật ở cuối mặt phẳng nghiêng là: \(v = \sqrt {2al}  = \sqrt {2.5.10}  = 10m/s\)

+ Gia tốc của vật trên mặt phẳng ngang là: \(a' =  - \dfrac{{{F_{ms}}}}{m} =  - \dfrac{{\mu mg}}{m} =  - \mu g =  - 0,1.10 =  - 1m/{s^2}\)

+ Thời gian vật đi trên mặt phẳng ngang là: \(t' = \dfrac{{v' - v{'_0}}}{{a'}} = \dfrac{{0 - v}}{{a'}}\)  (do vật dừng lại nên \(v' = 0\) )

Ta suy ra: \(t' = \dfrac{{ - v}}{{a'}} = \dfrac{{ - 10}}{{ - 1}} = 10s\)