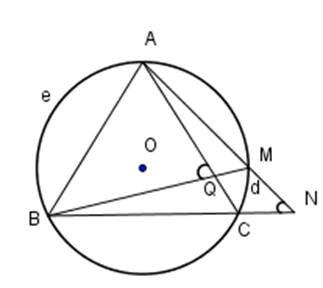
Từ điểm \(M\) nằm ngoài đường tròn \(\left( O \right)\) vẽ hai tiếp tuyến \(MA, MB\) với \(\left( O \right)\) tại \(A\) và \(B.\) Qua \(A\) vẽ đường thẳng song song với \(MB\) cắt đường tròn tại \(C.\)
.PNG)
Nối \(C\) với \(M\) cắt đường tròn \(\left( O \right)\) tại \(D.\) Nối \(A\) với \(D\) cắt \(MB\) tại \(E.\) Chọn câu đúng
Trả lời bởi giáo viên
Xét \(\Delta ABE\) và \(\Delta BDE\) có:
+ \(\widehat E\) chung.
+ \(\widehat {BAE} = \widehat {DBE}\) (góc nội tiếp và góc giữa tia tiếp tuyến và dây cung cùng chắn cung $BD$ )
Do đó ta có \(\Delta ABE \backsim \Delta BDE\,\left( {g.g} \right)\).
\( \Rightarrow \dfrac{{AE}}{{BE}} = \dfrac{{BE}}{{DE}} \Rightarrow E{B^2} = AE.DE\,\,\left( 1 \right).\)
Ta có: \(MB//AC \Rightarrow \widehat {EMD} = \widehat {DCA}\) (hai góc so le trong)
Mà \(\widehat {DCA} = \widehat {MAD}\) (góc nội tiếp và góc giữa tiếp tuyến và dây cung cùng chắn cung \(AD\))
Do đó \(\widehat {EMD} = \widehat {MAD}\).
Xét \(\Delta MEA\) và \(\Delta DEM\) có:
\(\widehat E\) chung.
\(\widehat {EMD} = \widehat {MAD}\) (cmt)
Suy ra \(\Delta MEA \backsim \Delta DEM\,.\)
Do đó
\(\dfrac{{ME}}{{DE}} = \dfrac{{EA}}{{EM}} \Rightarrow M{E^2} = DE.EA\,\,\left( 2 \right).\)
Từ \(\left( 1 \right)\) và \(2\) ta nhận được \(E{B^2} = E{M^2} \Rightarrow EB = EM.\)
Hướng dẫn giải:
Sử dụng tính chất góc nội tiếp và góc giữa tiếp tuyến và dây cung cùng chắn 1 cung.
Sử dụng tính chất tam giác đồng dạng.