Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa $24$ $g$ hương liệu, $9$ lít nước và $210$ $g$ đường để pha chế nước cam và nước táo.
+ Để pha chế $1$ lít nước cam cần $30$ $g$ đường, $1$ lít nước và $1$ $g$ hương liệu;
+ Để pha chế $1$ lít nước táo cần $10$ $g$ đường, $1$ lít nước và $4$ $g$ hương liệu.
Mỗi lít nước cam nhận được $60$ điểm thưởng, mỗi lít nước táo nhận được $80$ điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để đạt được số điểm thưởng cao nhất?
Trả lời bởi giáo viên
Giả sử $x,{\rm{ }}y$ lần lượt là số lít nước cam và số lít nước táo mà mỗi đội cần pha chế.
Suy ra $30x + 10y$ là số gam đường cần dùng;
$x + y$ là số lít nước cần dùng;
$x + 4y$ là số gam hương liệu cần dùng.
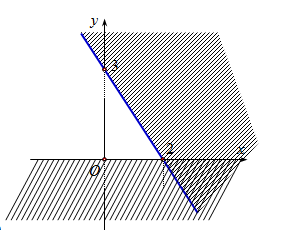
Theo giả thiết ta có $\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\30x + 10y \le 210\\x + y \le 9\\x + 4y \le 24\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\y \ge 0\\3x + y \le 21\\x + y \le 9\\x + 4y \le 24\end{array} \right..$ \(\left( * \right)\)
Số điểm thưởng nhận được sẽ là $P\left( {x;y} \right) = 60x + 80y.$
Ta đi tìm giá trị nhỏ nhất của biểu thức \(P\) với \(x,{\rm{ }}y\) thỏa mãn \(\left( * \right)\).

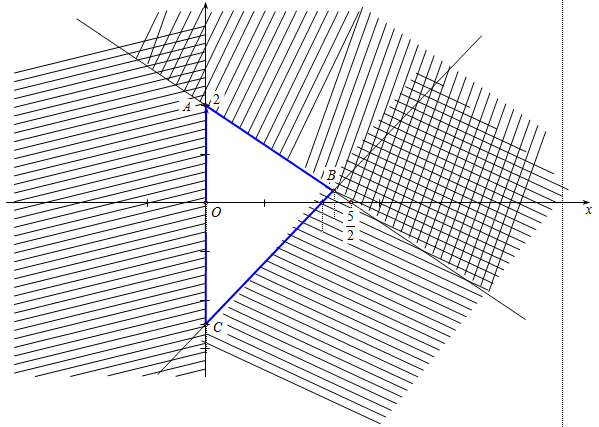
Miền nghiệm là phần hình vẽ không tô màu ở hình trên, hay là ngũ giác \(OBCDE\) với \(O\left( {0;0} \right),B\left( {0;6} \right),C\left( {4;5} \right),D\left( {6;3} \right),E\left( {7;0} \right)\).
Biểu thức $P = 60x + 80y$ đạt GTLN tại \(\left( {x;y} \right)\) là tọa độ một trong các đỉnh của ngũ giác.
Thay lần lượt tọa độ các điểm \(O,B,C,D,E\) vào biểu thức \(P\left( {x;y} \right)\) ta được:
\(P\left( {0;0} \right) = 0;P\left( {0;6} \right) = 480;P\left( {4;5} \right) = 640;P\left( {6;3} \right) = 600;P\left( {7;0} \right) = 420\)
Hướng dẫn giải:
- Gọi $x,{\rm{ }}y$ lần lượt là số lít nước cam và số lít nước táo mà mỗi đội cần pha chế.
- Biểu diễn số gam đường, số lít ngước, số gam hương liệu cần dùng theo \(x,y\).
- Sử dụng dữ kiện bài cho để lập hệ bất phương trình ẩn \(x,y\).
- Xác định miền nghiệm của bất phương trình trên mặt phẳng tọa độ.
- Xác định hàm số điểm thưởng nhận được \(F\left( {x;y} \right)\) và tìm \(\max F\left( {x;y} \right)\).