Đề mẫu ĐGNL 2019
Một bác nông dân cần trồng lúa và khoai trên diện tích đất gồm 6 ha, với lượng phân bón dữ trữ là 100kg và sử dụng tối đa 120 ngày công. Để trồng 1 ha lúa cần sử dụng 20kg phân bón, 10 ngày công với lợi nhuận là 30 triệu đồng, để trồng 1 ha khoai cần sử dụng 10 kg phân bón, 30 ngày công với lợi nhuận là 60 triệu đồng. Để đạt được lợi nhuận cao nhất, bác nông dân đã trồng \(x\left( {ha} \right)\) lúa và \(y\left( {ha} \right)\) khoai. Giá trị của \(x\) là:
Trả lời bởi giáo viên
Bước 1:
Gọi \(x,y\) (ha) lần lượt là diện tích đất cây trồng lúa và khoai \(\left( {x,y > 0} \right)\).
Tổng diện tích lúa và khoai được trồng là \(x + y\) (ha).
Tổng lượng phân bón cần dùng là \(20x + 10y\) (kg).
Tổng số ngày công cần dùng là \(10x + 30y\) (ngày).
Lợi nhuận thu được là \(S\left( {x;y} \right) = 30x + 60y\) (triệu đồng)
Từ giả thiết ta được hệ bất phương trình thể hiện miền nghiệm là:
\(\left\{ \begin{array}{l}x + y \le 6\\20x + 10y \le 100\\10x + 30y \le 120\\x \ge 0\\y \ge 0\end{array} \right.\)
Bước 2:
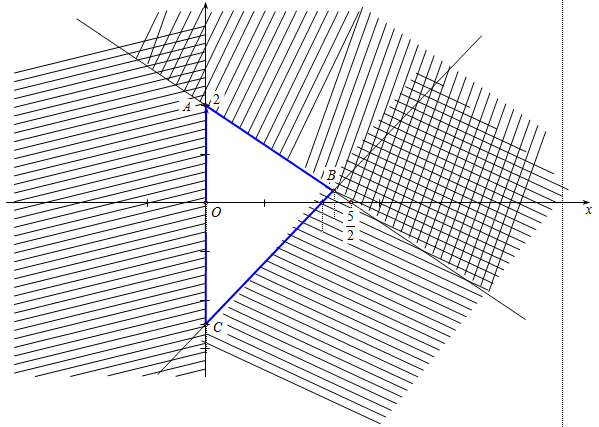
Ta biểu thị miền nghiệm của hệ bất phương trình bởi bằng đồ thị:

Miền nghiệm của hệ bất phương trình là ngũ giác \(OABCD\) vớ \(O\left( {0;0} \right),A\left( {0;4} \right),B\left( {3;3} \right),C\left( {4;2} \right),D\left( {5;0} \right)\).
Bước 3:
Khi đó \(S\left( {x;y} \right)\) đạt giá trị lớn nhất tại một trong các điểm O, A, B, C, D.
Ta có:
\(\begin{array}{l}S\left( O \right) = S\left( {0;0} \right) = 30.0 + 60.0 = 0\\S\left( A \right) = S\left( {0;4} \right) = 30.0 + 60.4 = 240\\S\left( B \right) = S\left( {3;3} \right) = 30.3 + 60.3 = 270\\S\left( C \right) = S\left( {4;2} \right) = 30.4 + 60.2 = 240\\S\left( D \right) = S\left( {5;0} \right) = 30.5 + 60.0 = 150\end{array}\)
Ta thấy \(S\left( {3;3} \right) = 270\) là giá trị lớn nhất khi \(x = y = 3\).
Vậy \(x = 3\).
Hướng dẫn giải:
Bước 1: Đưa về lập hệ bất phương trình bậc nhất hai ẩn.
Bước 2: Biểu diễn miền nghiệm của hệ bất phương trình tìm được .
Bước 3: Từ đó tìm giá trị lớn nhất của lợi nhuận.