Trong không gian $O x y z$, cho hai điểm \(A(2;1;3)\) và \(B(6;5;5)\). Xét khối nón \((N)\) có đỉnh \(A\), đường tròn đáy nằm trên mặt cầu đường kính $A B$. Khi \((N)\) có thể tích lớn nhất thì mặt phẳng chứa đường tròn đáy của \((N)\) có phương trình dạng \(2x + by + cz + d = 0\). Giá trị của \(b + c + d\) bằng

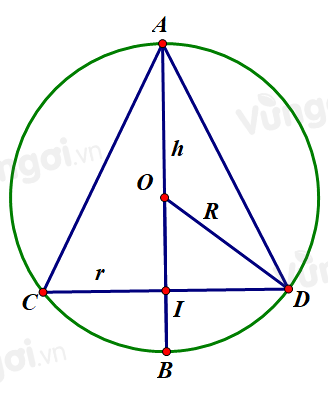
- Xét bài toán tổng quát: Cho khối nón \((N)\) có đỉnh \(A\), đáy có tâm là \(I\), bán kính r và chiều cao h nội tiếp mặt cầu \((S)\) có tâm \(O\), bán kính \(R\). Tìm thể tích lớn nhất của khối nón.

Để \({V_N}\) max thì ta xét \(h \ge R\) (vì nếu \(h < R\) thì đối xứng đường tròn đáy của (\(N\)) qua tâm \(O\), ta có bán kính đáy giữ nguyên nhưng chiều cao tăng lên).

Khi đó \(OI = h - R\) và

\({r^2} = {R^2} - {(h - R)^2} = h(2R - h)\)\(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi (2R - h){h^2}\)

Theo bất đẳng thức Cô-si thì \((2R - h) \cdot \dfrac{h}{2} \cdot \dfrac{h}{2} \le {\left( {\dfrac{{2R}}{3}} \right)^3}\) nên \(V \le \dfrac{{8\pi {R^3}}}{{81}}\). Giá trị lớn nhất này đạt được khi \(2R - h = \dfrac{h}{2} \Leftrightarrow h = \dfrac{{4R}}{3}\).

Áp dụng kết quả trên, để \({V_{(N)}}\) max thì \(I \in AB\) sao cho \(AI = \dfrac{{4R}}{3} = \dfrac{{2AB}}{3}\) hay \(\overrightarrow {AI}  = \dfrac{2}{3}\overrightarrow {AB}  = \dfrac{2}{3}(4;4;2) = \left( {\dfrac{8}{3};\dfrac{8}{3};\dfrac{4}{3}} \right)\), trong đó I là tâm đường tròn đáy.

=> \(I\left( {\dfrac{{14}}{3};\dfrac{{11}}{3};\dfrac{{13}}{3}} \right)\).

Ta cũng có mặt phẳng cần tìm vuông góc với $AB$ tại $I$ nên mặt phẳng cần tìm có phương trình

\(2\left( {x - \dfrac{{14}}{3}} \right) + 2\left( {y - \dfrac{{11}}{3}} \right) + \left( {z - \dfrac{{13}}{3}} \right) = 0\)\( \Leftrightarrow 2x + 2y + z - 21 = 0\)

Vì thế \((b,c,d) = (2,1, - 21)\) nên \(b + c + d =  - 18\).