Trả lời bởi giáo viên
Đáp án đúng: b
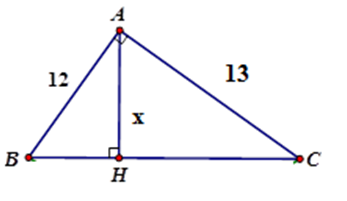
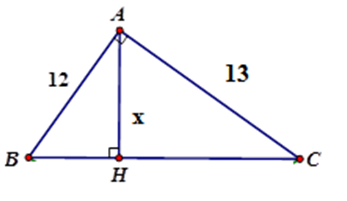
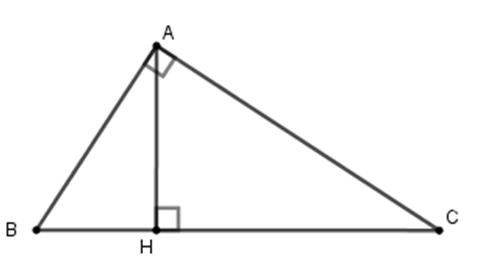
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông $ABC$ ta có:
$\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}$
\( \Leftrightarrow \dfrac{1}{{A{H^2}}} = \dfrac{{A{B^2} + A{C^2}}}{{A{B^2}.A{C^2}}} \)\(\Leftrightarrow A{H^2} = \dfrac{{A{B^2}.A{C^2}}}{{A{B^2} + A{C^2} }}\)
$ \Rightarrow AH = \dfrac{{AB.AC}}{{\sqrt {A{B^2} + A{C^2}} }} = \dfrac{{12.13}}{{\sqrt {{{12}^2} + {{13}^2}} }} \approx 8,82$
Vậy $x \approx 8,82$.
Hướng dẫn giải:
Tính $x$ theo hệ thức lượng $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}$
Câu hỏi khác
- Đề kiểm tra giữa học kì 1 - đề số 1 Toán 9 có lời giải chi tiết
- Đề kiểm tra giữa học kì 1 - đề số 2 Toán 9 có lời giải chi tiết
- Đề kiểm tra giữa học kì 1 - đề số 3 Toán 9 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 - đề số 1 Toán 9 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 - đề số 2 Toán 9 có lời giải chi tiết
