Câu hỏi:
2 năm trước
Tìm tập giá trị nhỏ nhất, giá trị lớn nhất của hàm số sau \(y = \dfrac{{{{\sin }^2}2x + 3\sin 4x}}{{2{{\cos }^2}2x - \sin 4x + 2}}\)
Trả lời bởi giáo viên
Đáp án đúng: d
Bước 1:
Ta có \({\sin ^2}2x = \dfrac{{1 - \cos 4x}}{2}\) và \(2{\cos ^2}2x = 1+\cos 4x\).
Khi đó \(y = \dfrac{{\dfrac{{1 - \cos 4x}}{2} + 3\sin 4x}}{{1 + \cos 4x - \sin 4x + 2}}\)
\(\Leftrightarrow y = \dfrac{{1 + 6.\sin 4x - \cos 4x}}{{2.\cos 4x - 2.\sin 4x + 6}}\)
Bước 2:
\( \Leftrightarrow 2y.\cos 4x - 2y.\sin 4x + 6y\)\( = 1 + 6.\sin 4x - \cos 4x\) \( \Leftrightarrow \left( {2y + 1} \right).\cos 4x - \left( {2y + 6} \right).\sin 4x = 1 - 6y\) \( \Rightarrow [\left( {2y + 1} \right).\cos 4x - \left( {2y + 6} \right).\sin 4x ]^2\)\(= (1 - 6y)^2\) (*)
Bước 3:
Áp dụng bất đẳng thức Bunhiacopxki, ta có \({\left[ {\left( {2y + 1} \right).\cos 4x - \left( {2y + 6} \right).\sin 4x} \right]^2} \le [{\left( {2y + 1} \right)^2} + (-{\left( {2y + 6} \right))^2}]. (\cos^2 4x + \sin^2 4x)\) $={\left( {2y + 1} \right)^2} + {\left( {2y + 6} \right)^2}$
Bước 4:
Kết hợp với (*), ta được \({\left( {1 - 6y} \right)^2} \le {\left( {2y + 1} \right)^2} + {\left( {2y + 6} \right)^2}\)
\(\begin{array}{l}1 - 12y + 36{y^2} \le 4{y^2} + 4y + 1 + 4{y^2} + 24y + 36\\ \Leftrightarrow 36{y^2} - 12y + 1 \le 8{y^2} + 28y + 37\\ \Leftrightarrow 28{y^2} - 40y - 36 \le 0\\ \Leftrightarrow 7{y^2} - 10y - 9 \le 0\end{array}\)
\( \Leftrightarrow \dfrac{{5 - 2\sqrt {22} }}{7} \le y \le \dfrac{{5 + 2\sqrt {22} }}{7}\)
Vậy \(\min y = \dfrac{{5 - 2\sqrt {22} }}{7}\); \(\max y = \dfrac{{5 + 2\sqrt {22} }}{7}\)
Hướng dẫn giải:
Bước 1: Sử dụng công thức hạ bậc làm xuất hiện các giá trị lượng giác \(\sin 4x,\cos 4x\).
Công thức hạ bậc: \({\sin ^2}x = \dfrac{{1 - \cos 2x}}{2}\) và \(2{\cos ^2}x = 1+\cos 2x\).
Bước 2: Đưa về dạng $a. \sin 4x+b.\cos 4x=c$
Bước 3: Áp dụng bất đẳng thức Bunhiacopxki : $(a.c+b.d)^2 \le (a^2+b^2).(c^2+d^2)$
Sử dụng công thức $\sin^2 x+\cos^2 x=1$
Bước 4: Giải bất phương trình ẩn y tìm min và max.
Cách bấm máy tính giải bất phương trình bậc 2:
(1): Ấn nút mode
(2): Ấn nút mũi tên chỉ xuống
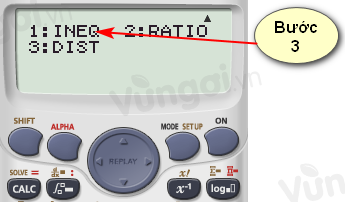
(Bước 3): Ấn số 1
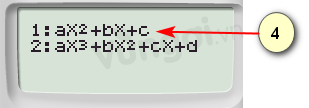
(4): Ấn tiếp số 1 để chọn bậc của BPT
(5): Ấn số 4 để chọn dạng BPT
Sau khi chọn chế độ giải bất phương trình bậc nhất một ẩn rồi thì ta thay hệ số của bất phương trình cần giải vào và ấn dấu "="
Câu hỏi khác
- Đề kiểm tra 1 tiết chương 1: Hàm số lượng giác và phương trình lượng giác - đề số 3 Toán 11 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 1: Hàm số lượng giác và phương trình lượng giác - đề số 1 Toán 11 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 1: Hàm số lượng giác và phương trình lượng giác - đề số 2 Toán 11 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 1: Hàm số lượng giác và phương trình lượng giác - đề số 3 Toán 11 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 1: Hàm số lượng giác và phương trình lượng giác - đề số 2 Toán 11 có lời giải chi tiết
