Câu hỏi:
2 năm trước
Tại thời điểm t, điện áp \(u = 200\sqrt 2 {\rm{cos}}\left( {100\pi t - \dfrac{\pi }{2}} \right)\) (trong đó u tính bằng V, t tính bằng s) có giá trị \(100\sqrt 2 \) và đang tăng. Sau thời điểm đó \(\dfrac{7}{{600}}s\), điện áp này có giá trị là:
Trả lời bởi giáo viên
Đáp án đúng: a
Góc quay từ t đến \(\dfrac{7}{{600}}s\) : \(\Delta \varphi = \omega \Delta t = 100\pi \dfrac{7}{{600}} = \dfrac{{7\pi }}{6}(ra{\rm{d}})\)
Xác định các điểm trên vòng tròn lượng giác, ta được:
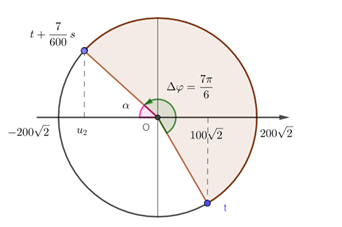
Từ vòng tròn ta có:
Tại thời điểm: \(t + \dfrac{7}{{600}}s\): điện áp có giá trị: \({u_2} = - {U_0}cos\alpha \)
Ta có: \(\alpha = \dfrac{\pi }{6}\left( {rad} \right) \to {u_2} = - {U_0}cos\dfrac{\pi }{6} = - 200\sqrt 2 cos\dfrac{\pi }{6} = - 100\sqrt 6 V\)
Hướng dẫn giải:
+ Sử dụng biểu thức góc quét trong khoảng thời gian: \(\Delta \varphi = \omega \Delta t\)
+ Sử dụng vòng tròn lượng giác
Câu hỏi khác
- Đề kiểm tra 1 tiết chương 3: dòng điện xoay chiều - đề số 03 Lý 12 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 3: dòng điện xoay chiều - đề số 01 Lý 12 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 3: dòng điện xoay chiều - đề số 02 Lý 12 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 3: dòng điện xoay chiều - đề số 01 Lý 12 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 3: dòng điện xoay chiều - đề số 03 Lý 12 có lời giải chi tiết
