Câu hỏi:
2 năm trước
So sánh \(A = \dfrac{{{{2018}^{2018}} + 1}}{{{{2018}^{2019}} + 1}}\) và \(B = \dfrac{{{{2018}^{2017}} + 1}}{{{{2018}^{2018}} + 1}}\) .
Trả lời bởi giáo viên
Đáp án đúng: a
Dễ thấy \(A < 1\) nên:
\(A = \dfrac{{{{2018}^{2018}} + 1}}{{{{2018}^{2019}} + 1}} < \dfrac{{\left( {{{2018}^{2018}} + 1} \right) + 2017}}{{\left( {{{2018}^{2019}} + 1} \right) + 2017}}\)\( = \dfrac{{{{2018}^{2018}} + 2018}}{{{{2018}^{2019}} + 2018}} = \dfrac{{2018.\left( {{{2018}^{2017}} + 1} \right)}}{{2018.\left( {{{2018}^{2018}} + 1} \right)}}\)\( = \dfrac{{{{2018}^{2017}} + 1}}{{{{2018}^{2018}} + 1}} = B\)
Vậy \(A < B\)
Hướng dẫn giải:
Sử dụng tính chất so sánh: Nếu \(\dfrac{a}{b} < 1\) thì \(\dfrac{a}{b} < \dfrac{{a + m}}{{b + m}}\)
Câu hỏi khác
Câu 5:
Một cửa hàng bán kính ghi lại số kính bán được trong tháng bằng bảng số liệu sau:
Số kính bán được trong tháng
|
Màu kính |
Trắng |
Đen |
Xanh |
Trắng bạc |
Vàng kim |
|
Số lượng |
20 |
10 |
30 |
15 |
25 |
Sử dụng các biểu tượng sau để vẽ biểu đồ tranh
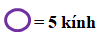
Cần bao nhiêu biểu tượng hình tròn màu tím để biểu diễn số kính màu vàng kim?
74
- Đề kiểm tra giữa kì 2 - đề số 2 Môn toán 6 sách Cánh diều có lời giải chi tiết
- Đề kiểm tra giữa kì 2 - đề số 1 Môn toán 6 sách Cánh diều có lời giải chi tiết
- Đề kiểm tra giữa kì 2 - đề số 5 Môn toán 6 sách Cánh diều có lời giải chi tiết
- Đề kiểm tra giữa kì 2 - đề số 3 Môn toán 6 sách Cánh diều có lời giải chi tiết
- Đề kiểm tra giữa kì 2 - đề số 4 Môn toán 6 sách Cánh diều có lời giải chi tiết
