Số nghiệm của phương trình \(\left| {1 - x} \right| - \left| {2x - 1} \right| = x - 2\) là
Trả lời bởi giáo viên
Ta có \(\left| {1 - x} \right| - \left| {2x - 1} \right| = x - 2\,\,\,\,\left( 1 \right)\)
Xét: \(\begin{array}{l} + )\;\;1 - x = 0 \Leftrightarrow x = 1\\ + )\;\;2x - 1 = 0 \Leftrightarrow x = \dfrac{1}{2}\end{array}\)
Ta có bảng xét dấu đa thức $1 - x$ và $2x - 1$ dưới đây
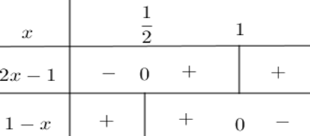
Từ bảng xét dấu ta có:
TH1: \(x < \dfrac{1}{2}\) khi đó \(\left| {2x - 1} \right| = 1 - 2x;\,\left| {1 - x} \right| = 1 - x\) nên phương trình \(\left( 1 \right)\) trở thành
\(1 - x - \left( {1 - 2x} \right) = x - 2 \Leftrightarrow 1 - x - 1 + 2x = x - 2 \Leftrightarrow x = x - 2\)
\( \Leftrightarrow 0 = - 2\) (vô lý)
TH2: \(\dfrac{1}{2} \le x \le 1\), khi đó \(\left| {2x - 1} \right| = 2x - 1;\,\left| {1 - x} \right| = 1 - x\) nên phương trình \(\left( 1 \right)\) trở thành
\(1 - x - \left( {2x - 1} \right) = x - 2 \Leftrightarrow - 3x + 2 = x - 2 \Leftrightarrow - 4x = - 4 \Leftrightarrow x = 1\,\left( {TM} \right)\)
TH3: \(x > 1\) , khi đó \(\left| {2x - 1} \right| = 2x - 1;\,\left| {1 - x} \right| = x - 1\) nên phương trình \(\left( 1 \right)\) trở thành
\(x - 1 - \left( {2x - 1} \right) = x - 2 \Leftrightarrow - x = x - 2 \Leftrightarrow 2x = 2 \Leftrightarrow x = 1\,\,\left( {L} \right)\)
Vậy phương trình có nghiệm \(x = 1\) .
Hướng dẫn giải:
- Lập bảng xét điều kiện bỏ dấu giá trị tuyệt đối.
- Căn cứ vào bảng xét từng khoảng giải bài toán (đối chiếu với điều kiện tương ứng).

