Trả lời bởi giáo viên
Bước 1:
Điều kiện:
\(1 - \sin 2x \ne 0 \Leftrightarrow \sin 2x \ne 1 \Leftrightarrow 2x \ne \dfrac{\pi }{2} + k2\pi \Leftrightarrow x \ne \dfrac{\pi }{4} + k\pi \,\,\left( {k \in Z} \right)\)
Bước 2:
\(\dfrac{{\cos 2x}}{{1 - \sin 2x}} = 0 \Leftrightarrow \cos 2x = 0 \Leftrightarrow {\cos ^2}2x = 0 \)
\(\Leftrightarrow {1-{\sin ^2}2x = 0} \Leftrightarrow {\sin ^2}2x = 1 \)\(\Leftrightarrow \sin 2x = - 1\) (vì \(\sin 2x \ne 1\))
\( \Leftrightarrow 2x = - \dfrac{\pi }{2} + k2\pi \Leftrightarrow x = - \dfrac{\pi }{4} + k\pi \)
Đặt $k=l+1 $ ta được:
\(- \dfrac{\pi }{4} + k\pi= - \dfrac{\pi }{4} + l\pi+\pi\)\(= \dfrac{{3\pi }}{4} + l\pi \left( {l \in Z} \right)\)
Vậy $x= \dfrac{{3\pi }}{4} + l\pi \left( {l \in Z} \right)$ hay $x= \dfrac{{3\pi }}{4} + k\pi \left( {l \in Z} \right)$
Hướng dẫn giải:
Bước 1: Tìm ĐKXĐ của phương trình.
Sử dụng công thức: $\sin x \ne 1 \Leftrightarrow x \ne \dfrac{\pi}{2}+k2\pi$
Bước 2: Giải phương trình tìm nghiệm và kiểm tra điều kiện.
Sử dụng công thức:
$\sin^2 x+\cos^2 x=1$
$\sin x = -1 \Leftrightarrow x =- \dfrac{\pi}{2}+k2\pi$
Giải thích thêm:
Một số em khi tính được \(x = - \dfrac{\pi }{4} + k\pi \) thì vội vàng chọn nhầm đáp án A là sai.
Một số em thì chỉ giải phương trình \(\cos 2x = 0 \Leftrightarrow 2x = \dfrac{\pi }{2} + k\pi \Leftrightarrow x = \dfrac{\pi }{4} + \dfrac{{k\pi }}{2}\) và không kiểm tra điều kiện xác định dẫn đến chọn nhầm đáp án B.
Cách biểu diễn và loại nghiệm bằng đường tròn đơn vị:
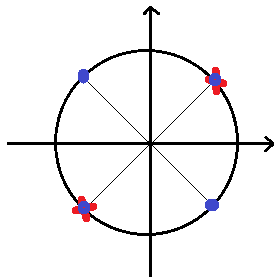
Bốn điểm màu xanh là biểu diễn góc lượng giác \(x = \dfrac{\pi }{4} + \dfrac{{k\pi }}{2}\), hai điểm gạch chéo màu đỏ là biểu diễn góc lượng giác \(x = \dfrac{\pi }{4} + k\pi \). Ta không lấy hai điểm này vì điều kiện xác định là \(x \ne \dfrac{\pi }{4} + k\pi \) nên chỉ còn lại hai điểm màu xanh đối xứng với nhau qua \(O\) nên biểu diễn góc lượng giác \(x = \dfrac{{3\pi }}{4} + k\pi \).

