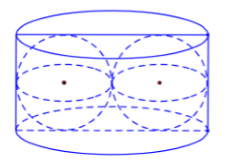
Người ta xếp hai quả cầu có cùng bán kính $r$ vào một chiếc hộp hình trụ sao cho các quả cầu đều tiếp xúc với hai đáy, đồng thời hai quả cầu tiếp xúc với nhau và mỗi quả cầu đều tiếp xúc với đường sinh của hình trụ (tham khảo hình vẽ). Biết thể tích khối trụ là $120\,\,c{m^3}$, thể tích của mỗi khối cầu bằng

Cho khối nón có độ dài đường cao bằng $2a$ và bán kính đáy bằng $a.$ Thể tích của khối nón đã cho bằng:

Cho hình chóp $SABCD$ có đáy $ABCD$ là hình vuông cạnh $a,\,\,SA = a$ và $SA \bot \left( {ABCD} \right).$ Thể tích khối chóp $SABCD$ bằng

Trong không gian $Oxyz,$ một vecto chỉ phương của đường thẳng $\Delta :\,\,\dfrac{{x - 1}}{1} = \dfrac{{y + 3}}{2} = \dfrac{{z - 3}}{{ - 5}}$ có tọa độ là:

Với $a,\,b$ là các số thực dương bất kì, ${\log _2}\dfrac{a}{{{b^2}}}$ bằng:

Trong không gian $Oxyz,$ cho hai điểm $A\left( { - 2; - 1;\,\,3} \right)$ và $B\left( {0;\,\,3;\,\,1} \right).$ Gọi $\left( \alpha  \right)$ là mặt phẳng trung trực của $AB.$ Một vecto pháp tuyến của $\left( \alpha  \right)$ có tọa độ là:

Cho cấp số nhân $\left( {{u_n}} \right)$ có ${u_1} = 1,\,\,{u_2} =  - 2.$ Mệnh đề nào sau đây đúng?

Hình dưới đây là đồ thị của hàm số nào?