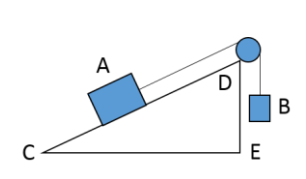
Người ta dùng vật B kéo vật A ( có khối lượng \({m_A} = 10kg\)) chuyển động đều đi lên mặt
phẳng nghiêng như hình bên. Biết \(CD = 4m,DE = 1m\). Bỏ qua ma sát, vật B phải có khối lượng bao nhiêu ?
Trả lời bởi giáo viên
Ta có,
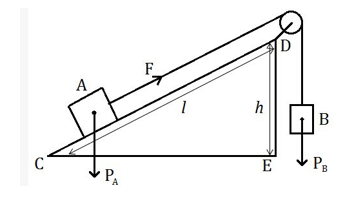
+ Tác dụng lên vật A có trọng lượng \({P_A}\) và lực kéo \(F\) của sợi dây có độ lớn bằng trọng lượng \({P_B}\) của vật B.
Do bỏ qua ma sát nên theo tính chất của mặt phẳng nghiêng ,ta có:
\(\frac{{{P_A}}}{F} = \frac{{CD}}{{DE}} = \frac{l}{h} \to \frac{{{P_A}}}{{{P_B}}} = \frac{l}{h}\)
Lại có: \(P = 10m\)
Ta suy ra:
\(\begin{array}{l}\frac{{{P_A}}}{{{P_B}}} = \frac{{{m_A}}}{{{m_B}}} = \frac{l}{h} = \frac{4}{1} = 4\\ \to {m_B} = \frac{{{m_A}}}{4} = \frac{{10}}{4} = 2,5kg\end{array}\)
Hướng dẫn giải:
+ Sử dụng tính chất của mặt phẳng nghiêng: \(\frac{P}{F} = \frac{l}{h}\)
+ Vận dụng biểu thức tính trọng lượng: \(P = 10m\)