Trả lời bởi giáo viên
Đáp án đúng: c
Bước 1:
Ta có: $\cos 3x = \cos x \Leftrightarrow \left[ \begin{array}{l}3x = x + k2\pi \\3x = - x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2x = k2\pi \\4x = k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = k\pi \\x = \dfrac{{k\pi }}{2}\end{array} \right. $
Bước 2:
+) Với họ nghiệm $x=k\pi$ ta có:
Khi $k=0$ thì $x=0$, điểm biểu diễn là điểm A (Vẫn là điểm đó khi k chẵn)
Khi $k=1$ thì $x=\pi$, điểm biểu diễn là A' (Vẫn là điểm đó khi k lẻ).
Như thế họ nghiệm $x=k\pi$ có $2$ điểm biểu diễn là $A,A'$.
+) Với họ nghiệm $x= \dfrac{{k\pi }}{2}$ ta có:
Khi $k=0$ thì $x=0$, điểm biểu diễn là điểm A (Vẫn là điểm đó khi k có dạng 4m, tức là k chia hết cho 4)
Khi $k=1$ thì $x= \dfrac{{\pi }}{2}$, điểm biểu diễn là B (Vẫn là điểm đó khi k có dạng 4m+1).
Khi $k=2$ thì $x= \pi$, điểm biểu diễn là A' (Vẫn là điểm đó khi k có dạng 4m+2).
Khi $k=3$ thì $x= \dfrac{{3\pi }}{2}$, điểm biểu diễn là B' (Vẫn là điểm đó khi k có dạng 4m+3).
Như thế họ nghiệm $x = \dfrac{{k\pi }}{2}$ có $4$ điểm biểu diễn là $A,A',B,B'$.
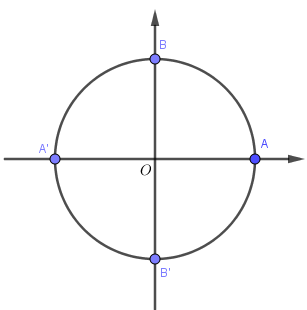
+) Kết hợp các điểm này lại ta được tổng cộng vẫn là 4 điểm $A,A',B,B'$. Mà 4 điểm này là 4 điểm biểu diễn của chính họ nghiệm $x = \dfrac{{k\pi }}{2}$ nên nghiệm của phương trình ban đầu là $x = \dfrac{{k\pi }}{2}$ $k \in Z$.
Hướng dẫn giải:
Bước 1: Áp dụng \(\cos x = \cos y \Leftrightarrow x = \pm y + k2\pi \) để giải phương trình.
Bước 2: Kết hợp nghiệm bằng đường tròn lượng giác.
Cách kết hợp:
+) Xét từng họ nghiệm và xác định điểm biểu diễn nghiệm trên đường tròn.
+) Tổng hợp các điểm biểu diễn và nhận xét vị trí tương quan giữa các điểm.
+) Các họ nghiệm có điểm biểu diễn cách đều:
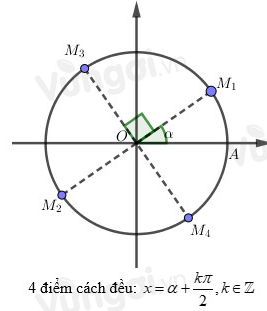
+) Xác định góc $\alpha$ (nếu cần thiết) như trên hình và kết luận.
Giải thích thêm:
Một số em có thể sẽ chọn nhầm đáp án A vì thay đáp án thấy A thỏa mãn nên chọn ngay A là sai.
Câu hỏi khác
- Đề kiểm tra 1 tiết chương 1: Hàm số lượng giác và phương trình lượng giác - đề số 3 Toán 11 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 1: Hàm số lượng giác và phương trình lượng giác - đề số 1 Toán 11 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 1: Hàm số lượng giác và phương trình lượng giác - đề số 2 Toán 11 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 1: Hàm số lượng giác và phương trình lượng giác - đề số 3 Toán 11 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 1: Hàm số lượng giác và phương trình lượng giác - đề số 2 Toán 11 có lời giải chi tiết
