Một viên đạn pháo đang bay ngang với vận tốc \({v_0} = 25{\rm{ }}m/s\) ở độ cao \(h = 80{\rm{ }}m\) thì nổ, vỡ làm hai mảnh, mảnh 1 có khối lượng \({m_1} = 2,5{\rm{ }}kg\), mảnh hai có \({m_2} = 1,5{\rm{ }}kg\). Mảnh một bay thẳng đứng xuống dưới và rơi chạm đất với vận tốc . Xác định độ lớn và hướng vận tốc của mảnh thứ hai ngay sau khi đạn nổ. Bỏ qua sức cản của không khí. Lấy \(g = 10m/{s^2}\)
Trả lời bởi giáo viên
Xét hệ gồm hai mảnh. Ngoại lực tác dụng lên hệ là trọng lực \(\overrightarrow P \), trọng lực này không đáng kể so với lực tương tác giữa hai mảnh. Do đó hệ được coi là hệ kín
Gọi \(\overrightarrow {{v_1}} \), \(\overrightarrow {{v_2}} \)lần lượt là vận tốc của mảnh 1 và mảnh 2 ngay sau khi vỡ.
Áp dụng định luật bảo toàn động lượng cho hệ, ta có:
\(\left( {{m_1} + {m_2}} \right)\overrightarrow {{v_0}} = {m_1}\overrightarrow {{v_1}} + {m_2}\overrightarrow {{v_2}} \) \(\left( 1 \right)\)
Theo đề bài: \(\overrightarrow {{v_1}} \) có chiều thẳng đứng hướng xuống, \(\overrightarrow {{v_0}} \) hướng theo phương ngang. Do đó ta có thể biểu diễn phương trình vectơ (1) như hình vẽ sau:
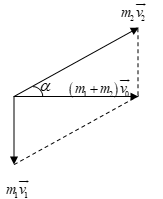
Theo đó:
\({m_2}{v_2} = \sqrt {{{\left[ {\left( {{m_1} + {m_2}} \right){v_0}} \right]}^2} + m_1^2v_1^2} \)\(\left( 2 \right)\)
\(\tan \alpha = \dfrac{{{m_1}{v_1}}}{{\left( {{m_1} + {m_2}} \right){v_0}}}\) \((3)\)
Để tính vận tốc của mảnh 1 ngay sau khi nổ ta áp dụng công thức: \(v{_1'^2} - v_1^2 = 2gh\)
\( \Rightarrow {v_1} = \sqrt {v{{_1'}^2} - 2gh} = \sqrt {{{90}^2} - 2.10.80} = 80,62m/s\)
Từ (2) ta tính được:
\({v_2} = \dfrac{{\sqrt {{{\left[ {\left( {{m_1} + {m_2}} \right){v_0}} \right]}^2} + m_1^2v_1^2} }}{{{m_2}}}\) \( \approx \)150m/s.
Từ (3), ta có: \(\tan \alpha = 2,015\)\( \Rightarrow \alpha = {64^0}\).
Như vậy ngay sau khi viên đạn bị vỡ, mảnh thứ 2 bay theo phương xiên lên trên hợp với phương ngang một góc 640.
Hướng dẫn giải:
Áp dụng công thức tính động lượng:\(\overrightarrow p = m\overrightarrow v \)
Áp dụng định luật bảo toàn động lượng
Áp dụng công thức trong chuyển động biến đổi

