Câu hỏi:
2 năm trước
Một vật dao động điều hoà với phương trình \(x = 4cos\left( {4\pi t + \dfrac{\pi }{6}} \right)cm\). Tìm số lần vật qua vị trí có gia tốc là \(32{\pi ^2}\left( {cm/{s^2}} \right)\) theo chiều âm trong thời gian \(5,75s\) tính từ thời điểm gốc.
Trả lời bởi giáo viên
Đáp án đúng: c
Ta có:
Chu kỳ dao động: \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{4\pi }} = 0,5{\rm{s}}\)
Tại $t = 0s$: \(\left\{ \begin{array}{l}x = 4c{\rm{os}}\left( {\dfrac{\pi }{6}} \right) = 2\sqrt 3 cm\\v = - A\omega \sin \left( {\dfrac{\pi }{6}} \right) < 0\end{array} \right.\)
Tại vị trí có \(a = 32{\pi ^2}cm/{s^2} = - {\omega ^2}{x_2} \to {x_2} = - \dfrac{{32{\pi ^2}}}{{{{\left( {4\pi } \right)}^2}}} = - 2cm\)
Trong một chu kỳ, vật đi qua vị trí $-2cm$ theo chiều âm $1$ lần
Ta có: \({\rm{5}}{\rm{,75s}} = 11T + \dfrac{T}{2}\)
Góc quét trong khoảng thời gian \(\dfrac{T}{2}\) kể từ thời điểm ban đầu:
\(\Delta \varphi = \omega .\Delta t = \dfrac{{2\pi }}{T}.\dfrac{T}{2} = \pi \)
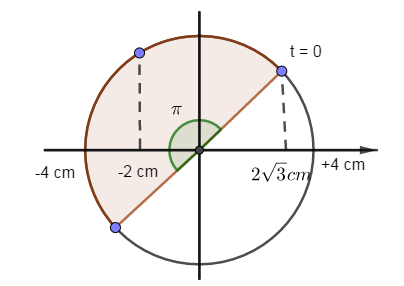
Trong khoảng thời gian \(\dfrac{T}{2}\) vật đi qua vị trí \( - 2cm\) theo chiều âm $1$ lần kể từ $t = 0$
=> Trong \(5,75s\) đầu tiên, vật qua vị trí \( - 2cm\) số lần là: \(11 + 1 = 12\) lần
Hướng dẫn giải:
+ Sử dụng công thức xác định chu kỳ T: \(T = \dfrac{{2\pi }}{\omega }\)
+ Xác định vị trí tại thời điểm $t = 0$ (x,v)
Câu hỏi khác
- Đề kiểm tra 15 phút chương 1: dao động cơ - đề số 01 Lý 12 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 1: dao động cơ - đề số 02 Lý 12 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 1: Dao động cơ - đề số 02 Lý 12 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 1: Dao động cơ - Đề số 01 Lý 12 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 1: dao động cơ - đề số 03 Lý 12 có lời giải chi tiết
