Câu hỏi:
2 năm trước
Một vật dao động điều hòa với chu kỳ \(T\) và biên độ \(A\). Khoảng thời gian ngắn nhất vật đi từ vị trí có động năng bằng thế năng đến vị trí có động năng bằng 3 lần thế năng là?
Trả lời bởi giáo viên
Đáp án đúng: d
Ta có:
+ Vị trí có động năng bằng thế năng:
\({{\rm{W}}_t} = {{\rm{W}}_{đ}} \to 2{{\rm{W}}_t} = {\rm{W}} \to {x_1} = \pm \dfrac{A}{{\sqrt 2 }}\)
+ Vị trí có động năng bằng 3 lần thế năng:
\({{\rm{W}}_d} = 3{{\rm{W}}_t} \to {{\rm{W}}_t} = \dfrac{{\rm{W}}}{4} \to {x_2} = \pm \dfrac{A}{2}\)
Xác định các vị trí trên vòng tròn lượng giác, ta được:
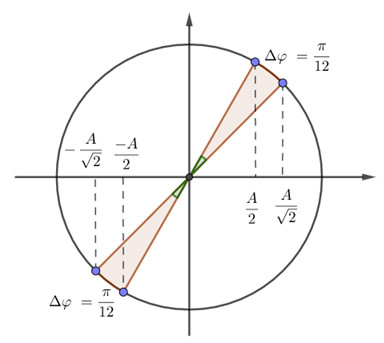
Thời gian ngắn nhất vật đi từ vị trí có động năng bằng thế năng đến vị trí có động năng bằng 3 lần thế năng tương ứng với góc quét: \(\Delta \varphi = \dfrac{\pi }{{12}}\)
Mặt khác,
\(\begin{array}{l}\Delta \varphi = \omega \Delta t \leftrightarrow \dfrac{\pi }{{12}} = \dfrac{{2\pi }}{T}.\Delta t\\ \to \Delta t = \dfrac{T}{{24}}\end{array}\)
Thời gian ngắn nhất vật đi từ vị trí có động năng bằng thế năng đến vị trí có động năng bằng 3 lần thế năng là \(\dfrac{T}{{24}}\)
Hướng dẫn giải:
+ Áp dụng biểu thức xác định cơ năng: \({\rm{W}} = {{\rm{W}}_t} + {{\rm{W}}_{\rm{d}}}\)
+ Sử dụng vòng tròn lượng giác và biểu thức: \(\Delta \varphi = \omega \Delta t\)
Câu hỏi khác
- Đề kiểm tra 15 phút chương 1: dao động cơ - đề số 01 Lý 12 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 1: dao động cơ - đề số 02 Lý 12 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 1: Dao động cơ - đề số 02 Lý 12 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 1: Dao động cơ - Đề số 01 Lý 12 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 1: dao động cơ - đề số 03 Lý 12 có lời giải chi tiết
