Câu hỏi:
2 năm trước
Một vật dao động điều hòa với chu kì $T{\rm{ }} = {\rm{ }}1s$. Tại thời điểm $t{\rm{ }} = {\rm{ }}0$, vật đi qua vị trí có li độ \(x = - 5\sqrt 2 cm\) với vận tốc \(v = - 10\pi \sqrt 2 cm/s\). Phương trình dao động của vật là:
Trả lời bởi giáo viên
Đáp án đúng: d
\(T = 1s \Rightarrow \omega = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{1} = 2\pi (rad)\)
Ta sử dụng phương trình độc lập theo thời gian của x và v để tìm biên độ dao động
\(A = \sqrt {{x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}} = \sqrt {{{\left( { - 5\sqrt 2 } \right)}^2} + \dfrac{{{{\left( { - 10\pi \sqrt 2 } \right)}^2}}}{{{{\left( {2\pi } \right)}^2}}}} = 10cm\)
Tai thời điểm ban đầu vật ở vị trí \(x = - 5\sqrt 2cm \) và có vận tốc âm nên khi biểu diễn trên đường tròn ta được pha ban đầu: \(\varphi = \dfrac{{3\pi }}{4}rad\)
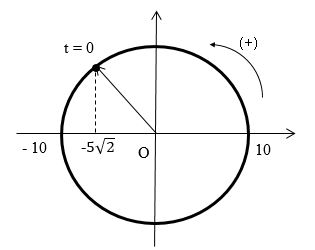
Khi đó ta có phương trình dao động là: \(x = A\cos (\omega t + \varphi ) = 10\cos (2\pi t + \dfrac{{3\pi }}{4})cm\)
Hướng dẫn giải:
+ Sử dụng biểu thức tính tần số góc: \(\omega = \dfrac{{2\pi }}{T}\)
+ Áp dụng hệ thức độc lập với thời gian của vận tốc và li độ: \({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}\)
+ Sử dụng đường tròn lượng giác xác định pha ban đầu
+ Viết phương trình dao động của vật: \(x = Acos\left( {\omega t + \varphi } \right)\)
Câu hỏi khác
- Đề kiểm tra 15 phút chương 1: dao động cơ - đề số 01 Lý 12 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 1: dao động cơ - đề số 02 Lý 12 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 1: Dao động cơ - đề số 02 Lý 12 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 1: Dao động cơ - Đề số 01 Lý 12 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 1: dao động cơ - đề số 03 Lý 12 có lời giải chi tiết
