Câu hỏi:
2 năm trước
Một sợi dây (không co giãn) được quấn đối xứng đúng 10 vòng quanh một ống trụ tròn đều có bán kính \(R = \dfrac{2}{\pi }\,\,cm\) (như hình vẽ).
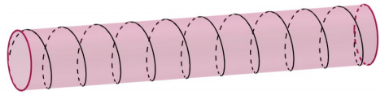
Biết rằng sợi dây có chiều dài 50 cm. Hãy tính diện tích xung quanh của ống trụ đó.
Trả lời bởi giáo viên
Đáp án đúng: d
Gọi độ dài đường cao của ống trụ là \(10x\,\,\left( {cm} \right)\,\,\left( {x > 0} \right)\).
Chia ống trụ thành 10 phần bằng nhau, mỗi phần có độ dài đường sinh là \(x\,\,\left( {cm} \right)\).
Trải phẳng mỗi ống trụ nhỏ ta được 1 hình chữ nhật có hai kích thước là \(x\) và \(2\pi .R = 2\pi .\dfrac{2}{\pi } = 4\,\,\left( {cm} \right)\).
Khi đó độ dài đường chéo của hình chữ nhật là \(\sqrt {{x^2} + {4^2}} = \sqrt {{x^2} + 16} \), và độ dài đường chéo chính bằng độ dài của 1 vòng.
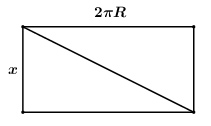
Do đó ta có phương trình: \(10\sqrt {{x^2} + 16} = 50 \Leftrightarrow \sqrt {{x^2} + 16} = 5\) \( \Rightarrow {x^2} + 16 = 25 \Leftrightarrow {x^2} = 9 \Leftrightarrow x = 3\,\,\left( {cm} \right)\,\,\left( {tm} \right)\).
\( \Rightarrow \) Độ dài đường cao của ống trụ là \(h = 10x = 30\,\,\left( {cm} \right)\).
Vậy diện tích xung quanh của ống trụ là \({S_{xq}} = 2\pi Rh = 2\pi .\dfrac{2}{\pi }.30 = 120\,\,\left( {c{m^2}} \right)\).
Hướng dẫn giải:
- Gọi độ dài đường cao của ống trụ là \(10x\,\,\left( {cm} \right)\,\,\left( {x > 0} \right)\).
- Chia ống trụ thành 10 phần bằng nhau, trải phẳng mỗi ống trụ nhỏ ta được 1 hình chữ nhật, xác định hai kích thước của hình chữ nhật đó.
- Độ dài đường chéo của hình chữ nhật là độ dài 1 vòng dây, lập phương trình tìm \(x\).
- Diện tích xung quanh hình trụ có chiều cao \(h\), bán kính đáy \(R\) là \({S_{xq}} = 2\pi Rh\).
