Trả lời bởi giáo viên
Đáp án đúng: d
* Giải từng bất phương trình ta được
+) \(2\left( {x - 1} \right) < x\)\( \Leftrightarrow 2x - 2 < x \)\(\Leftrightarrow 2x - x < 2 \)\(\Leftrightarrow x < 2\)
+) \(2\left( {x - 1} \right) \le x - 4 \)\(\Leftrightarrow 2x - 2 \le x - 4 \)\(\Leftrightarrow 2x - x \le - 4 + 2 \)\(\Leftrightarrow x \le - 2\)
+) \(2x < x - 4 \)\(\Leftrightarrow 2x - x < - 4 \)\(\Leftrightarrow x < - 4\)
+) \(2\left( {x - 1} \right) < x - 4 \)\(\Leftrightarrow 2x - 2 < x - 4 \)\(\Leftrightarrow 2x - x < - 4 + 2 \)\(\Leftrightarrow x < - 2\)
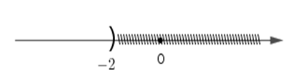
* Hình vẽ biểu diễn tập nghiệm \(S = \left\{ {x < - 2} \right\}\) .
Nên bất phương trình \(2\left( {x - 1} \right) < x - 4\) thỏa mãn.
Hướng dẫn giải:
+ Áp dụng quy tắc phá ngoặc, quy tắc chuyển vế và quy tắc nhân với một số để giải bất phương trình.
+ Dựa vào tập nghiệm được biểu diễn trên trục số để kết luận.
Câu hỏi khác
- Đề kiểm tra 45 phút chương 4: bất phương trình bậc nhất một ẩn - đề số 2 Toán 8 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 4: bất phương trình bậc nhất một ẩn - đề số 2 Toán 8 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 4: bất phương trình bậc nhất một ẩn - đề số 1 Toán 8 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 4: bất phương trình bậc nhất một ẩn - đề số 1 Toán 8 có lời giải chi tiết
