Câu hỏi:
2 năm trước
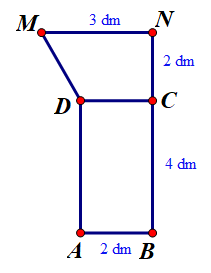
Hình dưới bao gồm hình chữ nhật $ABCD$ và hình thang vuông $CDMN$. Các điểm $B, C, N$ thẳng hàng, $A B=C N=2 \mathrm{dm} ; $$ B C=4 \mathrm{dm}; $$ M N=3 \mathrm{dm}$. Quay hình bên xung quanh cạnh $B N$ ta được khối tròn xoay có thể tích bằng
Trả lời bởi giáo viên
Đáp án đúng:
$\dfrac{86 \pi}{3} \mathrm{dm}^{3}$
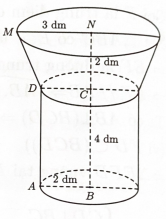
Bước 1: Xác định các hình khối khi quay hình quanh cạnh BN
Khi quay hình trên quanh cạnh $B N$ ta được một khối tròn xoay gồm một khối trụ có bán kính đáy bằng $2 \mathrm{dm}$, chiều cao bằng $4 \mathrm{dm}$ và một khối nón cụt có bán kính hai đáy lần lượt là $2 \mathrm{dm}$ và $3 \mathrm{dm}$, chiều cao bằng $2 \mathrm{dm}$.
Bước 2: Tính thể tích của từng hình (trụ+nón cụt) rồi tính tổng.
Thể tích khối trụ là $V_{T} =4 \pi .4$
Thể tích khối nón cụt là: $V_{N}=\dfrac{2}{3}(4 \pi+9 \pi+\sqrt{4 \pi .9 \pi}$
Do đó thể tích của khối tròn xoay là
$V=4 \pi .4+\dfrac{2}{3}(4 \pi+9 \pi+\sqrt{4 \pi .9 \pi})=\dfrac{86 \pi}{3}\left(\mathrm{dm}^{3}\right)$
Hướng dẫn giải:
Bước 1: Xác định các hình khối khi quay hình quanh cạnh BN
Bước 2: Tính thể tích của từng hình (trụ+nón cụt) rồi tính tổng.
