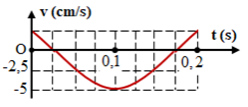
Hình bên là đồ thị biểu diễn sự phụ thuộc của vận tốc v theo thời gian t của một vật dao động điều hòa. Phương trình dao động của vật là
Trả lời bởi giáo viên
Từ đồ thị ta có:
+ Vận tốc cực đại: \({v_{ma{\rm{x}}}} = 5cm/s\)
+ \(\dfrac{T}{2} = 0,15{\rm{s}} \Rightarrow T = 0,3{\rm{s}} \Rightarrow \omega = \dfrac{{2\pi }}{T} = \dfrac{{20\pi }}{3}\left( {ra{\rm{d}}/s} \right)\)
Lại có: \({v_{ma{\rm{x}}}} = A\omega \Rightarrow A = \dfrac{{{v_{\max }}}}{\omega } = \dfrac{5}{{\dfrac{{20\pi }}{3}}} = \dfrac{3}{{4\pi }}cm\)
Tại \(t = 0:{v_0} = - A\omega \sin \varphi = 2,5cm/s\) và đang giảm
\( \Rightarrow \sin \varphi = - \dfrac{1}{2} \Rightarrow \varphi = - \dfrac{\pi }{6}\left( {ra{\rm{d}}} \right)\)
\( \Rightarrow \) Phương trình li độ dao động:
\(x = \dfrac{3}{{4\pi }}co{\rm{s}}\left( {\dfrac{{20\pi }}{3}t - \dfrac{\pi }{6}} \right)cm\)
Hướng dẫn giải:
+ Đọc đồ thị v – t
+ Sử dụng biểu thức vận tốc cực đại: \({v_{ma{\rm{x}}}} = A\omega \)
+ Viết phương trình li độ dao động điều hòa.


