Hàm số $y = \sqrt {\dfrac{{{x^3}}}{{\left| x \right| - 2}}} $ có tập xác định là:
Trả lời bởi giáo viên
Hàm số $y = \sqrt {\dfrac{{{x^3}}}{{\left| x \right| - 2}}} $ xác định nếu \(\dfrac{{{x^3}}}{{\left| x \right| - 2}} \ge 0\).
Ta có: \(\left| x \right| - 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 2\end{array} \right. ; x^3=0 \Leftrightarrow x=0\)
Xét dấu biểu thức \(\dfrac{{{x^3}}}{{\left| x \right| - 2}}\) ta có:
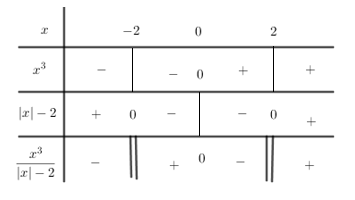
Khi đó tập xác định của hàm số là $\left( { - 2;0} \right] \cup \left( {2; + \infty } \right)$.
Hướng dẫn giải:
- Hàm số phân thức \(f\left( x \right) = \dfrac{1}{{P\left( x \right)}}\) xác định nếu \(P\left( x \right) \ne 0\).
- Hàm số căn thức \(\sqrt {P\left( x \right)} \) xác định nếu \(P\left( x \right) \ge 0\).
- Hàm số \(\sqrt {\dfrac{1}{{P\left( x \right)}}} \) xác định nếu \(P\left( x \right) > 0\).

