Hàm số \(y = f\left( x \right)\) có bảng biến thiên:
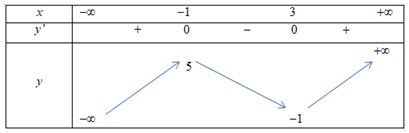
Phương trình \(f\left( {\left| {x - 1} \right|} \right) = 5\) có bao nhiêu nghiệm?
Chỉ được phép điền số 0, nguyên âm, nguyên dương và phân số dạng a/b
Đáp án:
Trả lời bởi giáo viên
Đáp án:
Đặt \(t = \left| {x + 1} \right|\left( {t \ge 0} \right)\)
Với \(t = 0 \Rightarrow x = - 1\)
Với \(t > 0 \Rightarrow \left| {x + 1} \right| = k > 0 \Leftrightarrow x = - 1 \pm k\)
Ta có: \(f\left( {\left| {x + 1} \right|} \right) = 5 \Leftrightarrow f\left( t \right) = 5\)
Lập bảng biến thiên:
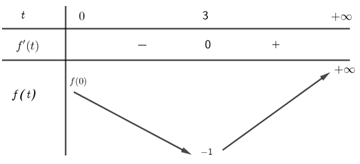
Do \(f\left( 0 \right) < 5\) nên dựa vào bảng biến thiên ta có: \(f\left( t \right) = 5\) có 1 nghiệm \({t_0} > 3\)
Khi đó phương trình \(\left| {x + 1} \right| = {t_0} > 3\) có 2 nghiệm.
\( \Rightarrow f\left( {\left| {x + 1} \right|} \right) = 5\) có 2 nghiệm.
Hướng dẫn giải:
- Đặt \(t = \left| {x + 1} \right|\left( {t \ge 0} \right)\)
- Đưa về hàm số biến t, lập bảng biến thiên
- Từ bảng biến thiên tìm số nghiệm t, sau đó tìm số nghiệm x.


