Hai hình bình hành \(ABCD\) và \(ABEF\) không cùng nằm trong một mặt phẳng. Trên cạnh \(AC\) lấy điểm \(M\) và trên cạnh \(BF\) lấy điểm \(N\) sao cho \(\dfrac{{AM}}{{AC}} = \dfrac{{BN}}{{BF}} = k\). Tìm \(k\) để \(MN//DE\).

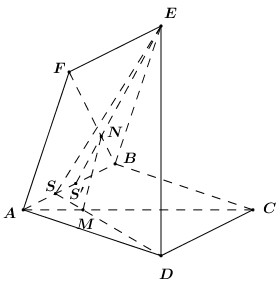
Trong \(\left( {ABCD} \right)\) gọi \(S = DM \cap AB\). Trong \(\left( {ABEF} \right)\) gọi \(S' = EN \cap AB\).

Để \(MN//DE\) thì \(M,\,\,N,\,\,D,\,\,E\) đồng phẳng.

Khi đó ta có: \(\left\{ \begin{array}{l}\left( {MNDE} \right) \cap \left( {ABCD} \right) = MS\\\left( {MNDE} \right) \cap \left( {ABEF} \right) = ES'\\\left( {ABCD} \right) \cap \left( {ABEF} \right) = AB\end{array} \right.\) \( \Rightarrow MS,\,\,ES',\,\,AB\) đồng quy.

\( \Rightarrow S \equiv S'\) hay \(DM,\,\,EN,\,\,AB\) đồng quy tại \(S\).

Khi đó ta có hình vẽ như sau:

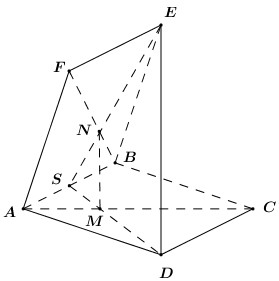
Áp dụng định lí Ta-lét ta có: \(\dfrac{{AM}}{{MC}} = \dfrac{{AS}}{{CD}} = \dfrac{{AS}}{{AB}}\); \(\dfrac{{BN}}{{NF}} = \dfrac{{BS'}}{{EF}} = \dfrac{{BS}}{{AB}}\).

Theo bài ra ta có: \(\dfrac{{AM}}{{AC}} = \dfrac{{BN}}{{BF}} \Rightarrow \dfrac{{AM}}{{AC - AM}} = \dfrac{{BN}}{{BF - BN}}\) \( \Rightarrow \dfrac{{AM}}{{MC}} = \dfrac{{BN}}{{BF}}\).

Từ đó suy ra \(\dfrac{{AS}}{{AB}} = \dfrac{{BS}}{{AB}} \Rightarrow AS = BS\) \( \Rightarrow S\) là trung điểm của \(AB\).

Khi đó ta có: \(\dfrac{{AM}}{{MC}} = \dfrac{{AS}}{{AB}} = \dfrac{1}{2} \Rightarrow \dfrac{{AM}}{{AM + MC}} = \dfrac{1}{{1 + 2}} \Rightarrow \dfrac{{AM}}{{AC}} = \dfrac{1}{3}\).

Vậy \(k = \dfrac{1}{3}\).