Để thiết kế một chiếc bể cá hình hộp chữ nhật không nắp có chiều cao là 60cm, thể tích là 96000 \({cm^3}\). Người thợ dùng loại kính để sử dụng làm mặt bên có giá thành 70.000 đồng/\({m^2}\) và loại kính để làm mặt đáy có giá thành 100.000 đồng/\({m^2}\). Tính chi phí thấp nhất để hoàn thành bể cá.
Chỉ được phép điền số 0, nguyên âm, nguyên dương và phân số dạng a/b
Đáp án:
Trả lời bởi giáo viên
Đáp án:
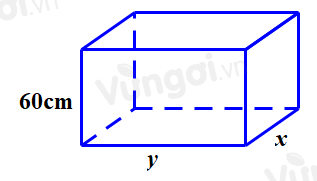
Gọi \(x\left( m \right),y\left( m \right)\left( {x > 0,y > 0} \right)\) là chiều dài và chiều rộng của đáy bể.
Theo bài ra, ta có: \(0,6xy = 0,096 \Leftrightarrow y = \dfrac{{0,16}}{x}\)
Diện tích của mặt đáy là: \({S_d} = x.y = x.\dfrac{{0,16}}{x} = 0,16\left( {{m^2}} \right)\)
Chi phí trả cho mặt đáy là: 0,16.100000=16000 đồng
Diện tích xung quanh của bể là: \({S_{xq}} = 2x.0,6 + 2y.0,6 = 1,2.\left( {x + y} \right)\)\( = 1,2.\left( {x + \dfrac{{0,16}}{x}} \right)\)
Chi phí để trả cho mặt xung quanh là: \(1,2.\left( {x + \dfrac{{0,16}}{x}} \right).70000 = 84000\left( {x + \dfrac{{0,16}}{x}} \right)\) đồng.
Tổng chi phí là:
\(\begin{array}{l}T\left( x \right) = 84\left( {x + \dfrac{{0,16}}{x}} \right) + 16000\\ \ge 84000.2\sqrt {x.\dfrac{{0,16}}{x}} + 16000 = 83200\end{array}\)
Vậy tổng chi phí thấp nhất là 83200 đồng.
Hướng dẫn giải:
- Gọi \(x\left( m \right),y\left( m \right)\left( {x > 0,y > 0} \right)\) lần lượt là chiều dài và chiều rộng của đáy bể.
- Tính chi phí của mặt đáy=S.100000
- Tính chi phí của tổng các mặt xung quanh=S.70000
- Sử dụng bất đẳng thức Cô-si để tính giá trị nhỏ nhất của tổng chi phí.


