Câu hỏi:
2 năm trước
Có bao nhiêu số nguyên \(m\) để phương trình \(x + 3 = m{e^x}\) có 2 nghiệm phân biệt?
Trả lời bởi giáo viên
Đáp án đúng: a
\(x + 3 = m{e^x} \Leftrightarrow m = \dfrac{{x + 3}}{{{e^x}}} = f\left( x \right)\,\,\left( * \right)\,\,\left( {Do\,\,{e^x} > 0\,\,\forall x \in \mathbb{R}} \right)\).
Để phương trình \(x + 3 = m{e^x}\) có 2 nghiệm phân biệt thì phương trình (*) có 2 nghiệm phân biệt.
Xét hàm số \(f\left( x \right) = \dfrac{{x + 3}}{{{e^x}}}\) ta có: \(f'\left( x \right) = \dfrac{{{e^x} - \left( {x + 3} \right){e^x}}}{{{e^{2x}}}} = \dfrac{{ - x - 2}}{{{e^x}}} = 0 \Leftrightarrow x = - 2\).
BBT:
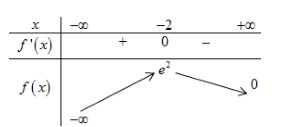
Số nghiệm của phương trình \(m = f\left( x \right)\) là số giao điểm của đồ thị hàm số \(y = m\) và \(y = f\left( x \right)\).
Dựa vào BBT ta có phương trình \(\left( * \right)\) có 2 nghiệm phân biệt \( \Rightarrow 0 < m < {e^2}\).
Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ {1;2;3;4;5;6;7} \right\}\).
Hướng dẫn giải:
+) Cô lập \(m\), đưa phương trình về dạng \(m = f\left( x \right)\).
+) Số nghiệm của phương trình \(m = f\left( x \right)\) là số giao điểm của đồ thị hàm số \(y = m\) và \(y = f\left( x \right)\).
+) Lập BBT hàm số \(y = f\left( x \right)\) và kết luận.
Câu hỏi khác
- Đề thi thử THPTQG môn Toán Chuyên ĐH Vinh Nghệ An lần 3 Toán 12 có lời giải chi tiết
- Đề thi thử THPTQG - Đề số 2 Toán 12 có lời giải chi tiết
- Đề thi thử THPTQG - Đề số 4 Toán 12 có lời giải chi tiết
- Đề thi thử THPTQG - Đề số 1 Toán 12 có lời giải chi tiết
- Đề tập huấn thi THPTQG Sở Giáo Dục và Đào Tạo Bắc Ninh 2019 Toán 12 có lời giải chi tiết
