Trả lời bởi giáo viên
Đáp án đúng: a
Vì n nguyên dương nên để 94n+1 nguyên thì 4n+1∈U(9)={±1;±3;±9}
Ta có bảng:
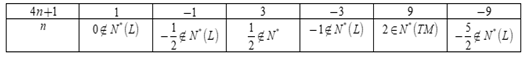
Vậy có duy nhất một giá trị của n thỏa mãn là n=2
Hướng dẫn giải:
Phân số ab(a,b∈Z,b≠0) là một số nguyên nếu b là ước của a
Giải thích thêm:
Một số em có thể sẽ chọn nhầm đáp án C vì nghĩ số 0 cũng là số nguyên dương hoặc D vì quên rằng n là số nguyên dương.
Câu hỏi khác
- Đề kiểm tra giữa kì 2 - đề số 1 Môn toán 6 sách CTST có lời giải chi tiết
- Đề kiểm tra giữa kì 2 - đề số 4 Môn toán 6 sách CTST có lời giải chi tiết
- Đề kiểm tra giữa kì 2 - đề số 1 Môn toán 6 sách CTST có lời giải chi tiết
- Đề kiểm tra giữa kì 2 - đề số 5 Môn toán 6 sách CTST có lời giải chi tiết
- Đề kiểm tra giữa kì 2 - đề số 2 Môn toán 6 sách CTST có lời giải chi tiết
