Trả lời bởi giáo viên
Đáp án đúng: c
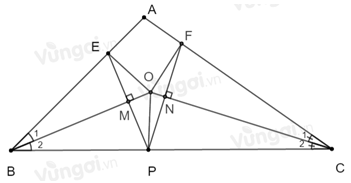
Giả sử \(EP \bot BO\) tại \(M\); \(PF \bot OC\) tại \(N\).
Khi đó \(\widehat {BME} = \widehat {BMP} = {90^0}\); \(\widehat {CNF} = \widehat {PNC} = {90^0}\)
Vì \(BO\) là tia phân giác của \(\widehat {ABC}\) (gt) nên \(\widehat {{B_1}} = \widehat {{B_2}}\) (tính chất tia phân giác)
Xét \(\Delta BME\) và \(\Delta BMP\) có:
\(\widehat {BME} = \widehat {BMP} = {90^0}\) (cmt)
\(BM\) là cạnh chung
\(\widehat {{B_1}} = \widehat {{B_2}}\) (cmt)
Do đó \(\Delta BME = \Delta BMP\) (g.c.g) suy ra \(ME = MP\) (hai cạnh tương ứng)
Mặt khác: \(EP \bot BO\) (gt)
Vậy \(OB\) là đường trung trực của đoạn \(EP\) (định nghĩa đường trung trực của đoạn thẳng). Đáp án A đúng.
Chứng minh tương tự ta có: \(\Delta CNF = \Delta CNP\) (g.c.g) suy ra \(NF = NP\) (hai cạnh tương ứng)
Mặt khác \(PF \bot OC\) (gt)
Vậy \(OC\) là đường trung trực của đoạn \(PF\) (định nghĩa đường trung trực của đoạn thẳng). Đáp án B đúng
Hướng dẫn giải:
+ Chứng minh \(\Delta BME = \Delta BMP\); \(\Delta CNF = \Delta CNP\), từ đó suy ra các cạnh tương ứng bằng nhau.
+ Sử dụng định nghĩa đường trung trực của đoạn thẳng: “Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng ấy tại trung điểm của nó” để đưa ra đáp án đúng.
Câu hỏi khác
- Đề kiểm tra 15 phút chương 7: quan hệ giữa các yếu tố trong tam giác. các đường đồng quy trong tam giác - đề số 2 Toán 7 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 7: quan hệ giữa các yếu tố trong tam giác. các đường đồng quy trong tam giác - đề số 1 Toán 7 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 7: quan hệ giữa các yếu tố trong tam giác. các đường đồng quy trong tam giác - đề số 1 Toán 7 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 7: quan hệ giữa các yếu tố trong tam giác. các đường đồng quy trong tam giác - đề số 2 Toán 7 có lời giải chi tiết
