Câu hỏi:
2 năm trước
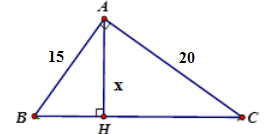
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\) có \(AC = 15\,cm,\,CH = 6\,cm\). Tính tỉ số lượng giác \(\cos B\).
Trả lời bởi giáo viên
Đáp án đúng: b
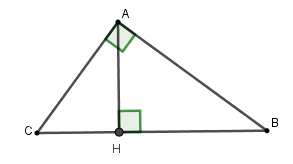
Xét tam giác \(AHC\) vuông tại \(H\), theo định lý Pytago ta có
\(A{H^2} = A{C^2} - C{H^2} = {15^2} - {6^2} = 189 \Rightarrow AH = 3\sqrt {21} \)
\( \Rightarrow \sin C = \dfrac{{AH}}{{AC}} = \dfrac{{3\sqrt {21} }}{{15}} = \dfrac{{\sqrt {21} }}{5}\)
Mà tam giác \(ABC\) vuông tại \(A\) nên \(\widehat B,\widehat C\) là hai góc phụ nhau. Do đó \(\cos B = \sin C = \dfrac{{\sqrt {21} }}{5}.\)
Hướng dẫn giải:
Bước 1: Tính cạnh cần thiết lại theo định lý Pytago hoặc hệ thức lượng trong tam giác vuông.
Bước 2: Sử dụng định nghĩa tỉ số lượng giác của góc nhọn. Sử dụng hai góc phụ nhau thì sin góc này bằng cosin góc kia.