Cho tam giác $ABC$ . Gọi $M,N$ lần lượt là trung điểm của các cạnh $AB,AC$ . Vẽ \(BP \bot MN;\,CQ \bot MN\,\left( {P,\,Q \in MN} \right)\) . So sánh \({S_{BPQC}}\) và \({S_{ABC}}\).

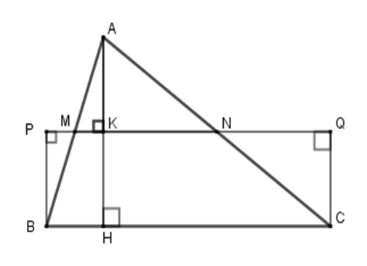
Kẻ \(AH \bot BC\) tại \(H\) và \(AH\) cắt \(MN\) tại \(K\) .

+ Xét tam giác \(ABC\) có \(MN\) là đường trung bình nên \(MN{\rm{//}}BC\) suy ra \(AH \bot MN\) tại \(K\) .

Xét tứ giác \(CBPQ\) có \(PQ{\rm{//}}BC\) (do \(MN{\rm{//}}BC\)) và \(PB{\rm{//}}CQ\) (do cùng vuông góc với \(PQ\) ) nên \(CBPQ\) là hình bình hành. Lại có \(\widehat {PBC} = 90^\circ \) nên tứ giác \(CBPQ\) là hình chữ nhật.

Suy ra \({S_{CBPQ}} = BP.BC\) .

+ Xét \(\Delta BPM\) và \(\Delta AKM\) có

Suy ra \(\Delta BPM = \Delta AKM\,\left( {ch - gn} \right) \Rightarrow BP = AK\) (hai cạnh tương ứng)  (1)

Xét \(\Delta ABK\) có \(MK{\rm{//}}BH\) (do\(MN{\rm{//}}BC\) ) và \(M\) là trung điểm của \(AB\) nên \(K\) là trung điểm của \(AH\) (định lý về đường trung bình của tam giác). Nên \(AK = \dfrac{1}{2}AH\)   (2).

Từ (1) và (2) ta có \(PB = \dfrac{1}{2}AH\) .

+ \({S_{ABC}} = \dfrac{1}{2}AH.BC\) mà \(PB = \dfrac{1}{2}AH\)(cmt) nên \({S_{ABC}} = PB.BC\) .

Lại có \({S_{CBPQ}} = BP.BC\) (cmt) nên ta có \({S_{ABC}} = {S_{CBPQ}}\) .