Câu hỏi:
3 năm trước
Cho tam giác $ABC$ cân tại đỉnh $A$ với \(\widehat A = {80^0}\). Trên hai cạnh $AB,AC$ lần lượt lấy hai điểm $D$ và $E$ sao cho $AD = AE.$ Phát biểu nào sau đây đúng nhất?
Trả lời bởi giáo viên
Đáp án đúng: d
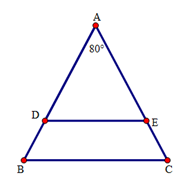
Ta có: \(\Delta ABC\) cân tại A suy ra \(\widehat B = \widehat C = \dfrac{{{{180}^0} - \widehat A}}{2} = \dfrac{{{{180}^0} - {{80}^0}}}{2} = {50^0}\)
Vì AD = AE nên \(\Delta ADE\) cân , suy ra \(\widehat {ADE} = \dfrac{{{{180}^0} - \widehat A}}{2} = \dfrac{{{{180}^0} - {{80}^0}}}{2} = {50^0}\)
Do đó \(\widehat B = \widehat {ADE}\) . Mà hai góc này ở vị trí đồng vị nên $ED//BC.$
Vậy cả A, B, C đều đúng.
Hướng dẫn giải:
Sử dụng tính chất tam giác cân, tính chất tổng các góc của một tam giác, dấu hiệu nhận biết hai đường thẳng song song.