Câu hỏi:
2 năm trước
Cho $\Delta ABC$ vuông tại $A,$ ${\rm{ }}AH \bot BC{\rm{ }}(H \in BC);AB{\rm{ }} = 9cm,$${\rm{ }}AH = 7,2cm,{\rm{ }}HC = 9,6cm.$
Tính cạnh $AC;BC.$
Trả lời bởi giáo viên
Đáp án đúng: c
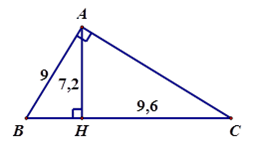
+) Xét $\Delta AHC$ vuông tại $H,$ theo định lý Py-ta-go ta có :
$\begin{array}{l}A{C^2} = A{H^2} + H{C^2}\\A{C^2} = 7,{2^2} + 9,{6^2}\\A{C^2} = 144\\ \Rightarrow AC = \sqrt {144} = 12cm\end{array}$
+) Xét \(\Delta ABC\) vuông tại $A,$ theo định lý Py-ta-go ta có:
$\begin{array}{l}B{C^2} = A{B^2} + A{C^2}\\B{C^2} = {9^2} + {12^2}\\B{C^2} = 225\\ \Rightarrow BC = \sqrt {225} = 15cm\end{array}$
Vậy \(AC = 12\,cm;BC = 15\,cm.\)
Hướng dẫn giải:
+) Áp dụng định lí Py-ta-go trong tam giác vuông $AHC$ ta tính được độ dài cạnh $AC$
+) Áp dụng định lí Py-ta-go trong tam giác vuông $ABC$ ta tính được độ dài cạnh $BC$
Câu hỏi khác
- Đề kiểm tra 15 phút chương 6: Tam giác - đề số 1 Toán 7 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 6: Tam giác - đề số 2 Toán 7 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 6: Tam giác - đề số 1 Toán 7 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 6: Tam giác - đề số 2 Toán 7 có lời giải chi tiết
