Câu hỏi:
2 năm trước
Cho số phức \(z = 2 - i + \dfrac{{ - 1 + i}}{{1 - 3i}}\). Giá trị của \(\left| z \right|\) bằng
Trả lời bởi giáo viên
Đáp án đúng: c
Sử dụng MTCT ta có \(z = 2 - i + \dfrac{{ - 1 + i}}{{1 - 3i}} = \dfrac{8}{5} - \dfrac{6}{5}i.\)
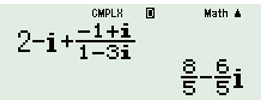
Vậy \(\left| z \right| = \sqrt {{{\left( {\dfrac{8}{5}} \right)}^2} + {{\left( { - \dfrac{6}{5}} \right)}^2}} = 2.\)
Hướng dẫn giải:
- Tính số phức z bằng MTCT.
- Số phức \(z = a + bi\) có môđun \(\left| z \right| = \sqrt {{a^2} + {b^2}} \).


