Cho khối trụ có hai đáy là \(\left( O \right)\) và \(\left( {O'} \right)\). \(AB,\,\,CD\) lần lượt là hai đường kính của \(\left( O \right)\) và \(\left( {O'} \right)\), góc giữa \(AB\) và \(CD\) bằng \({30^0}\), \(AB = 6\) và thể tích khối tứ diện \(ABCD\) bằng 30. Thể tích khối trụ đã cho bằng:
Trả lời bởi giáo viên
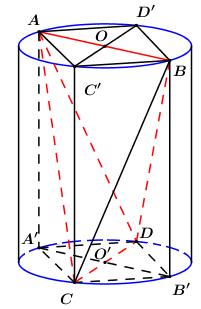
Gọi \(A',\,\,B'\) lần lượt là hình chiếu của \(A,\,\,B\) lên đường tròn \(\left( O \right)\).
\(C',\,\,D'\) lần lượt là hình chiếu của \(C,\,\,D\) lên đường tròn \(\left( {O'} \right)\).
\( \Rightarrow AC'BD'\) là hình bình hành, lại có \(AB = CD = C'D'\) nên \(AC'BD'\) là hình chữ nhật.
Khi đó \(AC'BD'.A'CB'D\) là hình hộp chữ nhật.
Ta có: \({V_{AC'BD'.A'CB'D}} = {V_{ABCD}} + {V_{A.A'CD}} + {V_{B.B'CD}} + {V_{C.C'AB}} + {V_{D.D'AB}}\).
Ta có: \({V_{A.A'CD}} = \dfrac{1}{3}AA'.{S_{A'CD}} = \dfrac{1}{3}AA'.\dfrac{1}{2}{S_{A'CB'D}} = \dfrac{1}{6}{V_{AC'BD'.A'CB'D}}\).
CMTT ta có: \({V_{B.B'CD}} = {V_{C.C'AB}} = {V_{D.D'AB}} = \dfrac{1}{6}{V_{AC'BD'.A'CB'D}}\).
\(\begin{array}{l} \Rightarrow {V_{AC'BD'.A'CB'D}} = {V_{ABCD}} + 4.\dfrac{1}{6}{V_{AC'BD'.A'CB'D}}\\ \Rightarrow {V_{ABCD}} = \dfrac{1}{3}{V_{AC'BD'.A'CB'D}} = 30\\ \Rightarrow {V_{AC'BD'.A'CB'D}} = 90\end{array}\)
Theo bài ra ta có: \(\angle \left( {AB;CD} \right) = {30^0} \Rightarrow \angle \left( {AB;C'D'} \right) = {30^0}\), giả sử \(\angle \left( {AB;C'D'} \right) = \angle AOC' = {30^0}\).
Lại có \(OA = OC' = \dfrac{1}{2}AB = 3\) \( \Rightarrow {S_{OAC'}} = \dfrac{1}{2}OA.OC'.\sin \angle AOC' = \dfrac{1}{2}.3.3.\sin {30^0} = \dfrac{9}{4}\).
\( \Rightarrow {S_{AC'BD'}} = 4{S_{OAC'}} = 9\).
Ta có: \({V_{AC'BD'.A'CB'D}} = AA'.{S_{AC'BD'}}\)\( \Rightarrow 90 = AA'.9 \Leftrightarrow AA' = 10\).
Vậy thể tích khối trụ là \(V = \pi {r^2}h = \pi .O{A^2}.AA' = \pi {.3^2}.10 = 90\pi \).
Hướng dẫn giải:
Gọi \(A',\,\,B'\) lần lượt là hình chiếu của \(A,\,\,B\) lên đường tròn \(\left( O \right)\).
\(C',\,\,D'\) lần lượt là hình chiếu của \(C,\,\,D\) lên đường tròn \(\left( {O'} \right)\).
- Phân chia khối đa diện: \({V_{AC'BD'.A'CB'D}} = {V_{ABCD}} + {V_{A.A'CD}} + {V_{B.B'CD}} + {V_{C.C'AB}} + {V_{D.D'AB}}\), chứng minh \({V_{A.A'CD}} = {V_{B.B'CD}} = {V_{C.C'AB}} = {V_{D.D'AB}} = \dfrac{1}{6}{V_{AC'BD'.A'CB'D}}\), từ đó tính \({V_{AC'BD'.A'CB'D}}\).
- Tính diện tích tam giác \(OAC'\), sử dụng công thức \({S_{OAC'}} = \dfrac{1}{2}OA.OC'.\sin \angle AOC'\), từ đó suy ra \({S_{AC'BD'}}\).
- Tính chiều cao \(AA'\): \(AA' = \dfrac{{{V_{AC'BD'.A'CB'D}}}}{{{S_{AC'BD'}}}}\).
- Tính thể tích khối trụ có chiều cao \(h\), bán kính đáy \(r\): \(V = \pi {r^2}h\).