Câu hỏi:
2 năm trước
Cho khối nón có độ dài đường sinh bằng \(2a\) và bán kính đáy bằng \(a\). Thể tích của khối nón đã cho bằng
Trả lời bởi giáo viên
Đáp án đúng: a
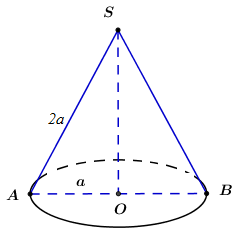
Xét \(\Delta SAO\) vuông tại \(O\) có: \(SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {{{\left( {2a} \right)}^2} - {a^2}} = a\sqrt 3 .\)
Khi đó ta có: \(V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi .{a^2}.a\sqrt 3 = \dfrac{{\pi {a^3}\sqrt 3 }}{3}.\)
Hướng dẫn giải:
+) Sử dụng công thức: \(h = \sqrt {{l^2} - {R^2}} .\)
+) Thể tích hình nón có bán kính R và đường cao h là: \(V = \dfrac{1}{3}\pi {R^2}h.\)