Cho khối chóp đều $S . A B C D$ có \(AC = 4a\), hai mặt phẳng \((SAB)\) và \((SCD)\) vuông góc với nhau. Thể tích của khối chóp đã cho bằng

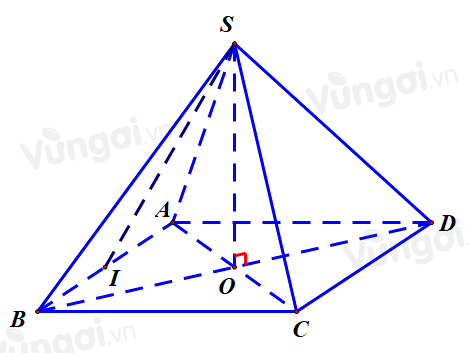
Gọi \(O\) là tâm hình vuông suy ra \(SO \bot (ABCD)\)

Ta có \((SAB) \cap (SCD) = Sx//AB//CD\)

Gọi \(I\) là trung điểm của $A B$

=> \(SI \bot AB \Rightarrow SI \bot Sx\)

\( \Rightarrow SI \bot (SCD) \Rightarrow SI \bot SD\)

\(AC = 4a \Rightarrow AD = 2\sqrt 2 a \Rightarrow DI = a\sqrt {10} \)

Đặt \(SD = x \Rightarrow SI = \sqrt {{x^2} - 2{a^2}} \).

Ta có hệ thức \({x^2} - 2{a^2} + {x^2} = 10{a^2}\) \( \Rightarrow {x^2} = 6{a^2} \Rightarrow x = a\sqrt 6 \)

Từ đó ta tính được \(SO = a\sqrt 2 \).

Vậy \({V_{S.ABCD}} = \dfrac{1}{3} \cdot a\sqrt 2  \cdot {(2\sqrt 2 a)^2} = \dfrac{{8\sqrt 2 }}{3}{a^3}\).