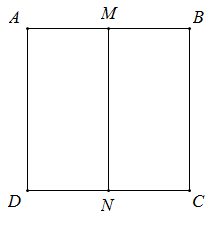
Cho hình vuông $ABCD$ có cạnh bằng $a$. Gọi $M,N$ lần lượt là trung điểm của $AB$ và $CD$. Khi quay hình vuông $ABCD$ quanh $MN$ tạo thành một hình trụ. Gọi $\left( S \right)$ là mặt cầu có diện tích bằng diện tích toàn phần của hình trụ, ta có bán kính của mặt cầu $\left( S \right)$ là:
Trả lời bởi giáo viên
Mặt trụ tạo bởi hình vuông $ABCD$ khi quay quanh $MN$ có chiều cao $h = a$ và bán kính đáy $r = \dfrac{a}{2}$ nên có diện tích toàn phần:
${S_{tp}} = 2\pi r\left( {r + h} \right) = 2\pi .\dfrac{a}{2}\left( {\dfrac{a}{2} + a} \right) = \dfrac{{3{a^2}\pi }}{2}$
Mặt cầu $\left( S \right)$ có diện tích bằng ${S_{tp}}$ của mặt trụ thì có bán kính $R$ với:
$4\pi {R^2} = \dfrac{{3{a^2}\pi }}{2} \Leftrightarrow R = \dfrac{{a\sqrt 6 }}{4}$
Hướng dẫn giải:
- Diện tích toàn phần hình trụ \({S_{tp}} = 2\pi rh + 2\pi {r^2}\)
- Diện tích mặt cầu \(S = 4\pi {R^2}\)