Câu hỏi:
2 năm trước
Cho hình trụ có các đáy là hình tròn tâm $O$ và tâm $O'$ , bán kính đáy bằng chiều cao và bằng $4cm$. Trên đường tròn đáy tâm $O$ lấy điểm $A$, trên đường tròn đáy tâm $O'$ lấy điểm B sao cho $AB = 4\sqrt 3 cm$. Thể tích khối tứ diện $AOO'B$ là:
Trả lời bởi giáo viên
Đáp án đúng: a
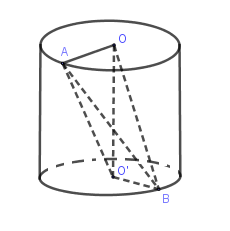
Tam giác \(OAO'\) vuông tại \(O\) nên:
\(O'A = \sqrt {O{A^2} + O'{O^2}} = \sqrt {{4^2} + {4^2}} = 4\sqrt 2 \)
Tam giác \(AO'B\) có:
\(O'{A^2} + O'{B^2} = A{B^2}\) nên tam giác \(AO'B\) vuông tại \(O'\)
Ta có $\left\{ \begin{array}{l}O'B \bot {\rm{OO'}}\\O'B \bot A{\rm{O'}}\end{array} \right. \Rightarrow O'B \bot \left( {{\rm{AOO'}}} \right)$
${S_{\Delta AOO'}} = \dfrac{1}{2}OA.OO= \dfrac{1}{2}.4.4 = 8$
$ \Rightarrow {V_{AOO'B}} = \dfrac{1}{3}{S_{\Delta AOO'}}.O'B = \dfrac{1}{3}.8.4 = \dfrac{{32}}{3}$
Hướng dẫn giải:
- Chứng minh \(O'B \bot \left( {AOO'} \right)\).
- Tính thể tích \({V_{AOO'B}} = {V_{B.AOO'}} = \dfrac{1}{3}{S_{\Delta AOO'}}.O'B\)
