Câu hỏi:
2 năm trước
Cho hình trụ bán kính đường tròn đáy bằng 1. Hai điểm \(A\) và \(B\) lần lượt thuộc hai đường tròn đáy sao cho \(AB = \sqrt 6 \), khoảng cách giữa hai đường thẳng \(AB\) và trục của hình trụ bằng \(\dfrac{1}{2}\). Thể tích khối trụ được giới hạn bởi hình trụ đó bằng:
Trả lời bởi giáo viên
Đáp án đúng: c
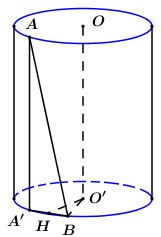
Gọi \(O,\,\,O'\) lần lượt là tâm đường tròn đáy chứa \(A,\,\,B\).
Gọi \(A'\) là hình chiếu của \(A\) lên đường tròn đáy chứa điểm \(B\).
Ta có \(AA'\parallel OO' \Rightarrow OO'\parallel \left( {AA'B} \right) \supset AB\) \( \Rightarrow d\left( {OO';AB} \right) = d\left( {OO';\left( {AA'B} \right)} \right) = d\left( {O';\left( {AA'B} \right)} \right)\).
Gọi \(H\) là trung điểm của \(A'B\), ta có \(O'H \bot A'B\) (quan hệ vuông góc giữa đường kính và dây cung).
Khi đó ta có: \(\left\{ \begin{array}{l}O'H \bot A'B\\O'H \bot AA'\end{array} \right. \Rightarrow O'H \bot \left( {AA'B} \right)\) \( \Rightarrow d\left( {OO';AB} \right) = OH = \dfrac{1}{2}\).
Áp dụng định lí Pytago trong tam giác vuông \(O'HB\) có \(HB = \sqrt {O'{B^2} - O'{H^2}} = \sqrt {{1^2} - {{\left( {\dfrac{1}{2}} \right)}^2}} = \dfrac{{\sqrt 3 }}{2}\).
\( \Rightarrow A'B = 2HB = \sqrt 3 \).
Áp dụng định lí Pytago trong tam giác vuông có: \(AA' = \sqrt {A{B^2} - A'{B^2}} = \sqrt {6 - 3} = \sqrt 3 \).
Vậy thể tích khối trụ là \(V = \pi {r^2}h = \pi {.1^2}.\sqrt 3 = \pi \sqrt 3 \).
Hướng dẫn giải:
- Gọi \(A'\) là hình chiếu của \(A\) lên đường tròn đáy chứa điểm \(B\). Sử dụng định lí: Khoảng cách giữa hai đường thẳng chéo nhau là khoảng cách giữa đường thẳng này và mặt phẳng song song chứa đường thẳng kia, chứng minh \(d\left( {OO';AB} \right) = d\left( {O';\left( {AA'B} \right)} \right)\).
- Gọi \(H\) là trung điểm của \(A'B\), chứng minh \(O'H \bot \left( {AA'B} \right)\).
- Sử dụng định lí Pytago trong tam giác vuông tính chiều cao của hình trụ.
- Thể tích khối trụ có chiều cao , bán kính đáy \(r\) là .
