Cho hình thang \(ABCD\) có \(AB\parallel CD\) và CD=2AB, E là trung điểm của BC. F là điểm thỏa mãn \(\overrightarrow {BF} = \dfrac{2}{3}\overrightarrow {AB} \). Tồn tại x sao cho \(\overrightarrow {MC} = x\overrightarrow {CD} \), tìm x để M, E, F thẳng hàng.
Trả lời bởi giáo viên
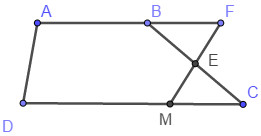
Ta có: M, E, F thẳng hàng nên theo hệ quả của định lí Ta-let ta có: \(\dfrac{{FE}}{{EM}} = \dfrac{{BE}}{{CE}} = \dfrac{1}{2}\) hay E là trung điểm của MF. Khi đó
\(\overrightarrow {MC} = \overrightarrow {BF} = \dfrac{2}{3}\overrightarrow {AB} = \dfrac{2}{3}.\dfrac{1}{2}\overrightarrow {DC} = \dfrac{1}{3}\overrightarrow {DC} = - \dfrac{1}{3}\overrightarrow {CD} \).
Vậy \(x = - \dfrac{1}{3}\)
Hướng dẫn giải:
Hệ quả của định lí Ta-let ta có: \(\dfrac{{FE}}{{EM}} = \dfrac{{BE}}{{CE}}=\dfrac{{BF}}{{CM}}\)