Cho hình lập phương $ABCD.A'B'C'D',AC$ và $BD$ cắt nhau tại $O,A'C'$ và $B'D'$ cắt nhau tại $O'$ . Các điểm $M,N,P$ theo thứ tự là trung điểm của $AB,BC,O'B'$. Khi đó thiết diện do mặt phẳng $\left( {MNP} \right)$ cắt hình lập phương sẽ là đa giác có số cạnh là bao nhiêu?
Trả lời bởi giáo viên
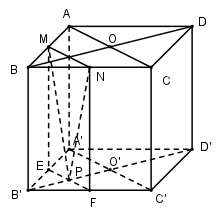
Ta có: $MN$ là đường trung bình của tam giác $ABC$ nên $MN//AC//A'C'$ .
$\left( {MNP} \right)$ và $\left( {A'B'C'D'} \right)$ có điểm $P$ chung và $MN//A'C'$ .
Qua $P$ kẻ \(EF//A'C';E \in A'B',F \in B'C'.\)
Vậy thiết diện của hình lập phương cắt bởi $mp\left( {MNP} \right)$ là $MNFE$.
Hướng dẫn giải:
Sử dụng tính chất: Nếu hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) có điểm chung $M$ và lần lượt chứa hai đường thẳng song song $d$ và $d'$ thì giao tuyến của \(\left( \alpha \right)\) và \(\left( \beta \right)\) là đường thẳng đi qua $M$ và song song với $d$ và $d'$.

