Cho hình hộp chữ nhật $ABCD.A'B'C'D' .$  Tính diện tích hình chữ nhật $ADC'B' \;$  biết $AB = 28cm,B' {D^2} = 3709,DD'  = 45cm.$

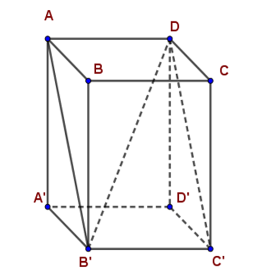
Xét tam giác $AA' B'$  vuông tại $A' $  có: $AA'  = DD'  = 45cm$  và $A' B'  = AB = 28cm$  

Áp dụng định lý Pytago ta có: 
$AA'^2 + A'B'^2 = AB'^2 $$\Leftrightarrow AB'= \sqrt {AA'^2 + A' B'^2}= 53cm$

Ta có: $AD \bot AA' ;AD \bot AB$  suy ra $AD \bot mp(AA' B' B) \Rightarrow AD \bot AB' $
Xét tam giác $ADB' $  vuông tại $A$ có: $AB'  = 53cm$  và $DB'^2 = 3709$  
Áp dụng định lý Pytago ta có: 
$A{D^2} + AB'^2 = DB'^2 \Leftrightarrow AD = \sqrt {DB'^2 - AB'^2} $ \( = \sqrt {3709 - {{53}^2}}  = 30\,cm\)

Vậy diện tích $ADC' B' $  bằng $AD.AB'  = 30.53 = 1590(c{m^2})$